SOLUTION: The largest interior angle of a kite is 140 °. Side measures are 1.6 m and 1.2 m. Determine the length of the shorter diagonal. Round to the tenths.

We want the shorter diagonal BD, 
but first we must calculate the longer diagonal, 
the green line AC below:



We use the law of cosines on ΔABC since this is the SAS case:

AC² = AB² + BC² - 2·AC·BC·cos(∠ABC)

AC² = 1.2² + 1.6² - 2(1.2)(1.6)cos(140°)

 AC = 2.634693656 m

We use the law of sines to find ∠BAC





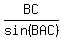
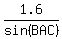
Cross multiply:

(2.634693656)sin(∠BAC) = (1.6)sin(140°)

             sin(∠BAC) = 

                  ∠BAC = 22.97645649°

Now that we have ∠BAC we draw half the shorter diagonal BE, 
which is perpendicular to the longer diagonal AC, in red:



Since ΔABE is a right triangle:

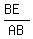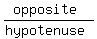 =  = sin(BAC)

BE = AB·sin(BAC)

BE = 1.2·sin(22.97645649°)

BE = 0.4684234191 m

So the entire shorter diagonal, BD, 



is twice the length of BE, so

BD = 2·BE = 2(0.4684234191) = 0.9368468381 m 

Rounded to tenths:  0.9 m

Edwin