SOLUTION: 3x^3-7x^2-43x+15 find all complex zeroes of the given polynomial function, and write the polynomial in completely factored form

Algebra ->  Polynomials-and-rational-expressions -> SOLUTION: 3x^3-7x^2-43x+15 find all complex zeroes of the given polynomial function, and write the polynomial in completely factored form       Log On


   

Question 763522: 3x^3-7x^2-43x+15
find all complex zeroes of the given polynomial function, and write the polynomial in completely factored form
Answer by josgarithmetic(39620) About Me  (Show Source):
You can put this solution on YOUR website!
Your possible values to check according to Rational Roots Theorem with synthetic division are PLUS AND MINUS OF these: { 5/3, 1/3, 5, 3, 1 }.

Greatly abbreviating the process here, You may find something about like this:
Checking 5, remainder 0, quotient 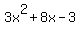3x%5E2%2B8x-3.
Checking -3, remainder 0, quotient 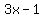3x-1.

The polynomial in factored form is 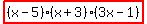highlight%28%28x-5%29%28x%2B3%29%283x-1%29%29.
The next zero based on the last binomial factor is +1%2F3, so the three roots or zeros are -3, 5, 1%2F3.

These are all Real zeros. They are also Complex zeros for which the imaginary compenents are zero.