Question 763000: Joanie got money from her uncle on every birthday. The amount of money he gives her is equal to her new age. (When she turned 5 he gave her $5, when she turned 7 he gave her $7, etc) She always put the money in a special box, rather than spend it. She now has $2145 in the box. How old is she?
Answer by ramkikk66(644)   (Show Source): (Show Source):
You can put this solution on YOUR website! If she is n years old, the money she would have got so far =
1+2+3+4....+n = 2145
The left side is an arithmetic progression with 1st term as 1, difference as 1 and n terms. (It is in fact the sum of the 1st n integers starting from 1)
It is given by n*(n+1)/2 = 2145

Simplifying, 
Factorizing:

n = -66, or n = 65.
Since age cannot be negative, Joanie is  years old. years old.
The above quadratic equation also be solved using the standard formula as shown below, which gives the solutions as n = -66 or n = 65.
:)
| Solved by pluggable solver: SOLVE quadratic equation with variable |
Quadratic equation  (in our case (in our case  ) has the following solutons: ) has the following solutons:

For these solutions to exist, the discriminant  should not be a negative number. should not be a negative number.
First, we need to compute the discriminant  : :  . .
Discriminant d=17161 is greater than zero. That means that there are two solutions:  . .


Quadratic expression 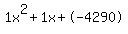 can be factored: can be factored:

Again, the answer is: 65, -66.
Here's your graph:
 |
|
|
|