Question 761459: solve x^3+5x^2-16x>80 in interval notation
I understand x^3+5x^2-16x-80>0...but I don't get from there...
Answer by josgarithmetic(39618)   (Show Source): (Show Source):
You can put this solution on YOUR website! You can use Rational Roots Theorem and perform synthetic divisions to find which roots are for the polynomial expression, and then test the intervals which the roots define.
First, find the factorization for 80.
80=2*2*2*2*5
so you want to check roots or plus and minus 2, 4, 8, 5, and 10, maybe 20, maybe 40.
When a synthetic division gives a remainder of zero, then the tested root is a root of the polynomial.
------
EDITED...Rechecked computation mistake...
Resorting to google tool, there should be found roots at -5, -4, and +4.
(One I did check but must have made a mistake, and other two I did not yet check).
Yes. _______-5 works, remainder=0 in synthetic division. The division result gives quotient x^2-16 which is factorable.

The intervals to check for the inequality are these:
(-infin,-5)
(-5, -4)
(-4, 4)
(4, +infin)
Testing each interval for which makes the inequality true you will find:
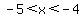 or or 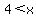
Either of those will work.
|
|
|