|
Question 76023:  is the equation. I don't know how to show that the 6x is squared to i just wrote it out. The way my teacher showed us to do this is with this as an example
2xsquared+5x-3=0 the 2xsquared and the -3 are factors, the 5x is the sum
(2x-1)(x+3)=0
2x-1=0 x+3=0 you can eliminate the -1 by adding 1 to each side and eliminate the 3 by -3 from each side. Leaving you with
2x=1 and x=-3 etc Now the way he showed us to check this is to multiply the first numbers in each equation ex. 2x*x this should give you your first factor of the equation, then the outer numbers ex. 2x*3 then the inner numbers ex. -1*x these added together should give you your sum and finally the last numbers ex. -1*3 this should give you your final factor. If you don't get the right numbers in the correct places or if your signs are mixed up it won't work. I have tried this equation in every way I know for example (6x+2)(x-1) this would make your original equation 6xsquared-4x-2, I tried (6x-2)(x+1) original equation would be 6xsquared+4-2, then i tried
(6x+1)(x-2) original equation would have to be 6xsquared-11x-2 and finally I tried (6x-1)(x+2) original equation would come out 6xsquared+11x-2 Please help me. Am I not getting something here I don't see any other way to do this. Thank you for your help. Cody
Answer by bucky(2189)   (Show Source):
You can put this solution on YOUR website! 
.
Cody, you have to look for combinations of numbers that involve all the factors of 6 and all
the factors of 2, and you have to also consider the signs of those factors. The factors
of the -2 are easy ... just 2 and 1. And you can tell that one of those numbers has to be
positive and one has to be negative ... so that when you multiply them together you get
-2, not +2. So now we can tell that our factors must be of the form:
.
(____ __ 2)*(____ __ 1)
.
and at this point we don't know which one is positive and which one is negative.
.
Now consider the possible factors of 6. Not only are there 6 and 1 which you used, but
there are also 3 and 2. You convinced yourself that 6x and 1x would not work. So now
you have to try 3x and 2x. Let's guess that the factors are:
.
(2x ___ 2)*(3x ___ 1)
.
The underlines are where we need to put the two signs ... one of them a + sign and the
other a - sign.
.
If you multiply 3x times 2 you get 6x and if you multiply 2x times 1 you get 2x. Is there
anyway that these two products can be added or subtracted to give the +x in the middle of
the original polynomial? Don't think so. So how about if we switch them around to get:
.
(3x ___ 2)*(2x ___ 1)
.
Then we multiply the 3x times the 1 and get 3x. And we multiply the 2x times the 2 and
get 4x. Is there anyway that you can add or subtract 3x and 4x and get +x? Sure is.
Suppose we had +4x - 3x. Those would add to give +x. So we need 2x times 2 to be positive.
That means that the 2 in the first set of parentheses needs to be positive, and if it is,
then the 1 in the second set of parentheses needs to be negative. So we can tell that
the factors need to be:
.
(3x + 2)*(2x - 1)
.
If you multiply these two factors out, you should find the product to be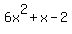 
as it was given in the original statement of the problem.
.
Use these two factors as a replacement for the left side of the equation in the original
problem and you get:
.
.
Notice that this equation will be true if either of the factors on the left side equals zero.
Why? Because multiplying by zero on the left side makes the entire left side equal to
zero which is equal to the right side.
.
Set the 3x + 2 on the left side equal to zero and solve for x:
.
3x + 2 = 0 <--- subtract 2 from both sides so you have only 3x on the left side.
.
3x = -2
.
Now divide both sides by 3, the multiplier of x, and you find that:
.
.
When then the factor 3x + 2 will be zero. That means the entire left side
of the equation will be zero, and will equal the right side of the equation.
.
You can, Cody, find another value for x that will make the left side of the equation
equal to zero. Find it by setting the other factor 2x -1 equal to zero.
.
2x - 1 = 0 <--- add + 1 to both sides to get rid of the -1 on the left side
.
2x = +1
.
Solve for x by dividing both sides by 2 to get:
.
.
So the two values for x that will satisfy the original equation are  and  .
.
Factoring is a useful way of solving the equation you get when you set a quadratic
polynomial equal to zero. There are a couple of more ways that you can find the values
for x that will satisfy the equation that results from setting a quadratic polynomial
equal to zero. One of those ways involves graphing the polynomial and finding where the
graph crosses the x-axis (if it does). Another way is called completing the square
and a third was is a variation of completing the square. It is involves using a special
equation that you will learn from your teacher ... called the quadratic formula.
.
Completing the square or using the quadratic formula involve less guess work than factoring
might, but if you can find the factors easily, it is generally a faster method than the other
processes. Keep after it, Cody. You seem to have the right ideas about factoring,
but you just needed to know that you might have to try all the factors of the first term
(the term that involves the squared variable).
|
|
|
| |
