Question 760068: In a list of consuctive odd integers, three times the first number is equal to three more than twice than twice the third number. Find the third number?
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! In a list of consecutive integers you may find
...., n-3, n-2, n-1, n, n+1, n+2, n+3, ...., in that order.
In a list of consecutive odd (or even) integers you find
...., n-6, n-4, n-2, n, n+2, n+4, n+6, ...., in that order.
So if the third of your consecutive odd integers were  , ,
the first would be 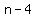 , and the second would be , and the second would be 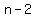 . .
Three times the first would be 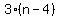 and and
three more than twice than twice the third number would be 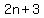
Then,  --> -->  --> -->  --> -->  --> --> 
|
|
|