SOLUTION: Find the sum of the squares of the three solutions of the equation x^3+(3x)^2-7x+1=0

Algebra ->  Equations -> SOLUTION: Find the sum of the squares of the three solutions of the equation x^3+(3x)^2-7x+1=0       Log On


   

Question 760067: Find the sum of the squares of the three solutions of the equation x^3+(3x)^2-7x+1=0
Answer by KMST(5328) About Me  (Show Source):
You can put this solution on YOUR website!
%283x%29%5E2=3%5E2%2Ax%5E2=9x%5E2 so x%5E3%2B%283x%29%5E2-7x%2B1=0 means x%5E3%2B9x%5E2-7x%2B1=0
You may have meant x%5E3%2B3x%5E2-7x%2B1=0, where only the x is squared.

THE PROBLEM AS POSTED:
Let the solutions of x%5E3%2B%283x%29%5E2-7x%2B1=0 be a, b, and c.
The full factorization of the polynomial 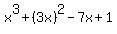x%5E3%2B%283x%29%5E2-7x%2B1 must be
x%5E3%2B%283x%29%5E2-7x%2B1=%28x-a%29%28x-b%29%28x-c%29
If we multiply that factorization we get

From that, we get
-%28a%2Bb%2Bc%29=9 --> a%2Bb%2Bc=-9 and
ab%2Bac%2Bbc=-7
If we multiply, we find that
%28a%2Bb%2Bc%29%5E2=a%5E2%2Bb%5E2%2Bc%5E2%2B2%28ab%2Bbc%2Bac%29
Replacing the values found for the polynomial,
%28-9%29%5E2=a%5E2%2Bb%5E2%2Bc%5E2%2B2%28-7%29 --> 81=a%5E2%2Bb%5E2%2Bc%5E2-14 --> a%5E2%2Bb%5E2%2Bc%5E2=81%2B14 --> a%5E2%2Bb%5E2%2Bc%5E2=95

IF THE PROBLEM EQUATION IS x%5E3%2B3x%5E2-7x%2B1=0:
Let the solutions of x%5E3%2B3x%5E2-7x%2B1=0 be a, b, and c.
The full factorization of the polynomial 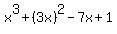x%5E3%2B%283x%29%5E2-7x%2B1 must be
x%5E3%2B3x%5E2-7x%2B1=%28x-a%29%28x-b%29%28x-c%29
If we multiply that factorization we get

From that, we get
-%28a%2Bb%2Bc%29=3 --> a%2Bb%2Bc=-3 and
ab%2Bac%2Bbc=-7
If we multiply, we find that
%28a%2Bb%2Bc%29%5E2=a%5E2%2Bb%5E2%2Bc%5E2%2B2%28ab%2Bbc%2Bac%29
Replacing the values found for the polynomial,
%28-3%29%5E2=a%5E2%2Bb%5E2%2Bc%5E2%2B2%28-7%29 --> 9=a%5E2%2Bb%5E2%2Bc%5E2-14 --> a%5E2%2Bb%5E2%2Bc%5E2=9%2B14 --> a%5E2%2Bb%5E2%2Bc%5E2=23