|
Question 760021: Please help me answer what is the Domain of the following equations and maybe some possible explanations as to how to get them/ arrive at the answer. The relations are as follows:
1) y= 7-3x
2) y= the square root of 5x+3
3) x^2 + y^2 is <_ (greater than or equal to) 9
4) y= the square root of 16-x^2
5) y= 2x/1-x^2
PLEASE REPLY ASAP because i want to learn how to arrive at the answer and the answer to these relations..
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! The domain is the set of possible values for x.
In the problems you posted there are no explicit restrictions to the domain, so we look for values of x that make the calculation impossible
1) y= 7-3x can be calculated for any real number x, so its domain ia all the real numbers
2)  can only be calculated when can only be calculated when
 <--> <-->  <--> <--> 
so the domain is the real numbers such that 
3)  (with a greater than or equal to sign) means points in the x-y plane that are at least 3 units away from the origin: (with a greater than or equal to sign) means points in the x-y plane that are at least 3 units away from the origin:
 That inequality determines a relation between x and y, but is a function That inequality determines a relation between x and y, but is a function  } that would assign a single value of y to each x value. For that relation, x can take any real value. } that would assign a single value of y to each x value. For that relation, x can take any real value.
You may have meant  (with a lesser than or equal to sign). That means points in the x-y plane that no more than 3 units away from the origin: (with a lesser than or equal to sign). That means points in the x-y plane that no more than 3 units away from the origin:
 That restricts the values of x to That restricts the values of x to 
4)  cannot be calculated as a real number if cannot be calculated as a real number if 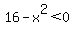 , so the domain is the x values that satisfy , so the domain is the x values that satisfy

Since  is the quadratic function with zeros at is the quadratic function with zeros at  and and  and a maximum in between at and a maximum in between at  , graphing like this , graphing like this
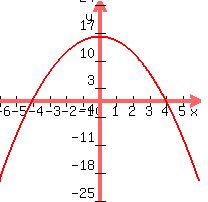 , ,  <--> <--> 
5) y= 2x/1-x^2 =  is not what you meant. is not what you meant.
You meant y = 2x/(1-x^2) =  . .
The expression  cannot be calculated when cannot be calculated when
 <--> <-->  
SO the domain for  is is
all the real numbers except  and and  . .
NOTE:
The horizontal line separating the  above it from the above it from the  below means that you have to calculate the expressions above and below the bar before you divide. When you cannot write below means that you have to calculate the expressions above and below the bar before you divide. When you cannot write  as you would on paper, you need to use parenteses to indicate the desired order of calculations. as you would on paper, you need to use parenteses to indicate the desired order of calculations.
As an analytical chemist, I have seen what happens if you do not enter the needed parentheses when using a calculator.
If I am trying to calculate  for for  , ,

The calculator would give me 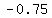 if I ask for if I ask for
2 X 3 ÷ ( 1 - 3 ^ 2 ) =
However, entering
2 X 3 ÷ 1 - 3 ^ 2 = will give me 
|
|
|
| |