Question 759942: A truck heads north at a constant speed of 80 km/h. A car leaves 20 minutes
later heading north along the same road and travelling at a constant speed of
90 km/h.
Write an equation that could be used to determine how much time in
hours, t, the car travels until it catches up to the truck.
**The correct answer is 90t = 80(t+1/3) , but I need help understanding why**
Found 2 solutions by josgarithmetic, MathTherapy:
Answer by josgarithmetic(39630)   (Show Source): (Show Source):
You can put this solution on YOUR website! The truck travels for 1/3 hour plus some unknown time, t.
Twenty minutes is 1/3 hour.
This distance is 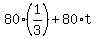 kilometers. kilometers.
The car, starting from the same departure point, travels for time, t, and catches-up with the truck.
This distance is  kilometers. kilometers.
Answer by MathTherapy(10556)   (Show Source): (Show Source):
You can put this solution on YOUR website!
A truck heads north at a constant speed of 80 km/h. A car leaves 20 minutes
later heading north along the same road and travelling at a constant speed of
90 km/h.
Write an equation that could be used to determine how much time in
hours, t, the car travels until it catches up to the truck.
**The correct answer is 90t = 80(t+1/3) , but I need help understanding why**
Let time it takes car to catch up to truck (get to meeting point) be T
Then time it'll take truck to get to meeting point = T + 1/3, since the truck will take a longer time to get to the meeting point as it's traveling at a slower speed
Distance car travels to get to meeting point = 90(T), or 90T
Distance truck travels to get to meeting point = 80(T + 1/3)
Both vehicles would've traveled the same distance, so: 
|
|
|