Question 75884: Please help me
tan(3x)+1={square root(2)}sec(3x)
so far i have tried:
(tan(3x)+1)^2=(sq rt(2))^2(sec(3x))^2
tan^2(9x^2)+1^2=2sec^2(9x^2)
tan^2 +1=2sec^2
tan^2+1 = sec^2
-------
2
I am totally confused now. This problem was assigned by my teacher.
We are using Trigonometry a Unit Circle Approach 7th edition
by Sullivan ISBN # 0-13-143111-0
Answer by kev82(151)   (Show Source): (Show Source):
You can put this solution on YOUR website! Hi,
Ok, the trick with these things until your comfortable with them is to get rid of the trigonometry as soon as possible and go back to good old fashioned algebra. To get rid of the trigonometry the first thing to do is write the equation in terms of only one trig function. I will choose ) , so we're trying to replace the secant with a tangent. , so we're trying to replace the secant with a tangent.
Obvioulsy we're after an identity connecting tangent and secant. How about this one?

You may ask, but in my equation I have ) This is easily solved by saying This is easily solved by saying 
So, hopefully you can rearrange the identity to get
 = \pm\sqrt{1+\tan^2(3x)})
Putting this into our equation gives
+1=\pm\sqrt{2}\sqrt{1+\tan^2(3x)})
Now let's get rid of that horrible tangent by saying )
This leaves us with the equation

We will now square both side, but remember that when we square the equation 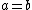 , we will also have the solutions to , we will also have the solutions to 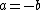 so you must check any solutions you get work in your original equation. so you must check any solutions you get work in your original equation.
Anyway, squaring gives

This rearanges nicely to

^2=0)
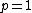
But we have solved for p, and we need to solve for x. Up above we defined
)
But, remember that tangent is a periodic function, and I can add or subtract integer multiples of  (we're working in radians right?) so the actual equation I want to solve is (we're working in radians right?) so the actual equation I want to solve is
=p=1, \forall n\in\mathbb{Z})
Taking inverse tangent and tidying up, we get
)
Leting n=0,1,2 gives the solutions  Don't forget to put these back in to your equation because when we squared we may have inadvertently considered solutions that don't solve our original equation. Question: if we didn't, can you say why not? Don't forget to put these back in to your equation because when we squared we may have inadvertently considered solutions that don't solve our original equation. Question: if we didn't, can you say why not?
Hope some of that was helpful,
Kev
|
|
|