SOLUTION: 3. Find the complex zeros of the polynomial function. Write f in factored form. F(x)=x^3-8x^2+29x-52 Use the complex zeros to write f in factored form F(x)=____(reduce fractions

Algebra ->  Functions -> SOLUTION: 3. Find the complex zeros of the polynomial function. Write f in factored form. F(x)=x^3-8x^2+29x-52 Use the complex zeros to write f in factored form F(x)=____(reduce fractions      Log On


   

Question 756643: 3. Find the complex zeros of the polynomial function. Write f in factored form.
F(x)=x^3-8x^2+29x-52
Use the complex zeros to write f in factored form
F(x)=____(reduce fractions and simplify roots)
Answer by Edwin McCravy(20055) About Me  (Show Source):
You can put this solution on YOUR website!
F(x)=x^3-8x^2+29x-52

The possible rational zeros are ± the factors of 52,
which are ±1,±2,±4,±13,±26, and ±52

You can keep trying those and the only one that gives
a zero remainder and is therefore a rational zero is 4.

4|1 -8  29 -52
 |   4 -16  52
  1 -4  13   0

So we have factored F(x) this way:

F(x) = (x-4)(x²-4x+13)

To find the other zeros we set the factor
x² - 4x + 13 = 0 and use the quadratic formula:


x = 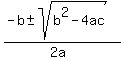%28-b+%2B-+sqrt%28+b%5E2-4ac+%29%29%2F%282a%29+

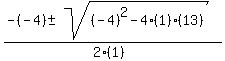x = %28-%28-4%29+%2B-+sqrt%28+%28-4%29%5E2-4%281%29%2813%29+%29%29%2F%282%281%29%29+ 

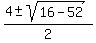x = %284+%2B-+sqrt%2816-52+%29%29%2F2+

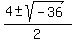x = %284+%2B-+sqrt%28-36+%29%29%2F2+

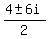x = %284+%2B-+6i%29%2F2+

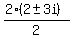x = %282%282+%2B-+3i%29%29%2F2+

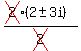x = %28cross%282%29%282+%2B-+3i%29%29%2Fcross%282%29+

x = 2 ± 3i

So the other zeros are 2 + 3i and 2 - 3i

So the factored form of F(x) is

F(x) = (x - 4)[x - (2 + 3i)][x - (2 - 3i)]

or 

F(x) = (x - 4)(x - 2 - 3i)(x - 2 + 3i)

Edwin