Question 756440: The equation of the circle with center at (-2,3) and tangent to the y-axis is
(x+2)^2+(y-3)^2=4
(x+2)^2+(y+3)^2=4
(x+2)^2+(y-3)^2=5
(x+2)^2+(y+3)^2=5
(x+2)^2+(y-3)^2=2
Can you please explain how you got the answer?
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website!  The tangent to a circle is perpendicular to the radius at the point of tangency. The tangent to a circle is perpendicular to the radius at the point of tangency.
Since the y-axis is vertical, at the point of tangency, rhe radius of a circle tangent to the y-axis must be horizontal.
The horizontal line that passes through point O(-2,3) is  , so , so
1) a radius of the circle with center at (-2,3) and tangent to the y-axis is contained in  , and , and
2) the point of tangency of the circle with center at (-2,3) and the y-axis is the intersection of  and the y-axis. and the y-axis.
That point of tangency is P(0,3).
The radius at that point is the segment OP, and its length is  . .
The equation of the circle with center at (-2,3) and radius 2 is
 --> --> 
because the equation of a circle with center at (h,k) and radius r is
 , ,
but you do not need to remember that formula because
1) you may know that the distance from a point (x,y) to point O(-2,3) is
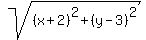 or or
2) you may apply the Pytagorean theorem to the right triangle in the figure below to find that 
  --> --> 
|
|
|