SOLUTION: write an equation of the ellipse with a vertex at (-8,0), a co-vertex at (0,4), and center at (0,0)

We plot those points, and sketch the ellipse:

      

Count the number of graph units there are between the center (0,0) 
and a vertex (-8,0). That's known as the "semi-major" axis, and its 
length is represented by the letter " a ".  So a = 8. [Incidentally
the ENTIRE major axis is 16 units long, it goes from one vertex (-8,0)
to the other vertex (8,0).]

Count the number of graph units there are between the center (0,0) 
and a covertex (0,4). That's known as the "semi-minor" axis, and its 
length is represented by the letter " b ".  So b = 4. [Incidentally
the ENTIRE minor axis is 8 units long, it goes from one covertex (0,4)
to the other covertex (0,-4).]

The equation of an ellipse that looks like this 

is    

          

where (h,k) is the center (0,0)  so h=0, k=0, and a=8, b=4

          

          

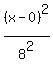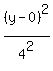
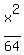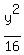Edwin