|
Question 75566: Can you please help me?
1. Write the equation of an ellipse with center (8, 7), horizontal major axis length 16, and minor axis length 4.
2. Write the equation of an ellipse with center (9, –3), horizontal major axis length 18, and minor axis length 10.
Thankyou
Answer by chitra(359)  (Show Source): (Show Source):
You can put this solution on YOUR website! The equation of the ellipse with center (h, k) is given by:
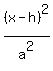 + + 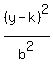 = 1 = 1
Where the length of the major axis is greater than the minor axis.
Here the centre is given by (8, 7) and
length of the major axis = 2a = 16
lenght of the minor axis = 2b = 4
This implies that a = 8 and b = 2
Hence, substituting these in the above formula, we have:
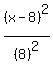 + + 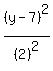 = 1 = 1
Simplifying these, we have:
 + + 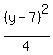 = 1 = 1
Taking LCM and simplifying this further, we have:
 = 64 = 64
Simplifying this again, we have:
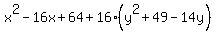 = 64 = 64
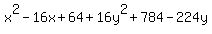 = 64 = 64
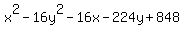 = 0 = 0
This is the equation of the ellipse.
-------------------------------------------------------------------------------
2. Write the equation of an ellipse with center (9, –3), horizontal major axis length 18, and minor axis length 10.
Solution:
The equation of the ellipse with center (h, k) is given by:
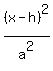 + + 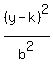 = 1 = 1
Where the length of the major axis is greater than the minor axis.
Here the centre is given by (9, -3) and
length of the major axis = 2a = 18
length of the minor axis = 2b = 10
This implies that a = 9 and b = 5
Hence, substituting these in the above formula, we have:
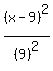 + + 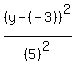 = 1 = 1
 + +  = 1 = 1
Taking LCM, we get:
 = 2025 = 2025
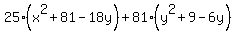 = 2025 = 2025
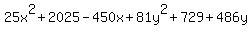 = 2025 = 2025
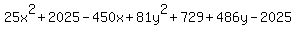 = 0 = 0

|
|
|
| |