SOLUTION: what are the x-intercepts of h? h(x)=(3x^4-54x^2+96x-45)/(2x^3-x^2-32x+16)

Algebra ->  Polynomials-and-rational-expressions -> SOLUTION: what are the x-intercepts of h? h(x)=(3x^4-54x^2+96x-45)/(2x^3-x^2-32x+16)      Log On


   

Question 755192: what are the x-intercepts of h?
h(x)=(3x^4-54x^2+96x-45)/(2x^3-x^2-32x+16)
Answer by KMST(5328) About Me  (Show Source):
You can put this solution on YOUR website!

The x-intercepts are the values of x that make h(x)=0.
Those would be the values that make x%5E4-18x%5E2%2B32x-15=0,
as long as they do not also make 2x%5E3-x%5E2-32x%2B16=0
If there are rational zeros for 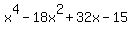x%5E4-18x%5E2%2B32x-15, they would be integers that are factors of 15.
The possible zeros are -15, -5, -3, -1, 1, 3, 5, and 15.
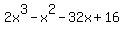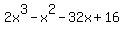The only ones of those that could be a zero of 2x%5E3-x%5E2-32x%2B16 are -1 and 1, which are factors of 16, but neither is a zero of 2x%5E3-x%5E2-32x%2B16.

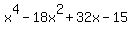ZEROS OF x%5E4-18x%5E2%2B32x-15:
highlight%28x=1%29 is obviously one of the zeros, since
1%5E4-18%2A1%5E2%2B32%2A1-15=1-18%2B32-15=0
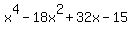x%5E4-18x%5E2%2B32x-15 divides exactly by %28x-1%29 twice, and we find that

Then, 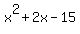x%5E2%2B2x-15 is easy to factor as
x%5E2%2B2x-15=%28x-3%29%28x%2B5%29
So the full factorization of 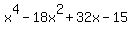x%5E4-18x%5E2%2B32x-15 is
x%5E4-18x%5E2%2B32x-15=%28x-1%29%5E2%28x-3%29%28x%2B5%29
So the x-intercepts of h(x), which are zeros of h(x) and of 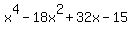x%5E4-18x%5E2%2B32x-15 are:
highlight%28x=1%29, highlight%28x=3%29, and highlight%28x=-5%29