|
Question 75462This question is from textbook
: How to write an equation of a line with the given slope and y-intercept?
1. m= 3/7 b=-2 2. m=9, b=0 3. m=0, b=-5
How to write an equation of a line through the given points
1. (-1,1) (2,7) 2. (0,-5)(3,-2) 3. (6,11) (3,13)
This question is from textbook
Answer by chitra(359)  (Show Source):
You can put this solution on YOUR website! How to write an equation of a line with the given slope and y-intercept?
1. m = 3/7 b = -2 2. m = 9, b = 0 3. m = 0, b =- 5
SOLUTION:
The general equation of the line is given by:
y = mx + b ----------------(1) represents the standard(general)equation.
where, m = represents the slope and b represents the y-intercept
1) m = 3/7 b = -2
Substituting these in the above equation, we have:
y = (3/7)x +(-2)
==> 7y = 3x - 14
-------------------------------------------------------------------------------
2. m = 9, b = 0
Substituting these values in the general eqn, we have:
y = (9)x + 0
==> y = 9x
------------------------------------------------------------------------------
3. m = 0, b =- 5
Substituting these values, we get:
y = (0)x + (-5)
==> y = - 5
------------------------------------------------------------------------------
(II) How to write an equation of a line through the given points
1. (-1,1) (2,7) 2. (0,-5)(3,-2) 3. (6,11) (3,13)
Solution: The equation of the line when two points are given is calculated by using the formula:
or this can also be written as :
(y - y1) = m (x - x1) ------------------(2)
Where  gives the slope of the eqn.
We first calculate the slope of the eqn and then substitute them in the eqn (2)
--------------------
--------------------
1. (-1,1) (2,7)
Here in this case m =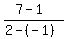 
==> m =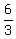 
==> m = 3
Substituting the point and the slope in the eqn (2), we get:
y - 1 = 3( x - (-1))
y - 1 = 3(x + 1)
y - 1 = 3x + 3
y = 3x + 4
----------------------------------------------
2. (0,-5)(3,-2)
Here in this case m =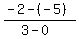 
==> m = 
==> m = 1
Substituting the point and the slope in the eqn (2), we get:
y - (-5) = 1( x - 0)
==> y + 5 = x is the equation of the straight line.
-----------------------------------------------------------------------------
3. (6,11) (3,13)
Here in this case the slope of this line is given by:
m = 
m =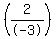 
Substituting this in the above formula, we get:
3y - 33 = -2x + 12
3y + 2x = 33 + 12
3y + 2x = 45
Hence, the solution.
HAPPY CALCULATING!!!!! :))
|
|
|
| |
