SOLUTION: Consider the following function f(x) = 2 sin(x/4 ? ?) What is the amplitude of this function? What is the exact period of f(x) (in radians)? (Recall ? radia

Meaning: The amplitude is the maximum positive number 
of units the graph rises above the x-axis (which is
also the positive number of units it falls below the 
x-axis.)

The period of a function is the pasitive distance
along the x-axis which spans one cycle of the graph.


Rule:


1. Compare graph to  to
   determine A, B, and C
2. Amplitude = 
3. Period = P = ÷
4. x-coordinate of starting point for basic cycle = S = ÷ 
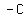5. Mark these five points on the x-axis:
   S, S+P/4, S+P/2, S+3P/4, S+P
6. Plot the 5 points:
   (S,0), (S+P/4,A), (S+P/2,0), (S+3P/4,-A), (S+P,0)
7. Draw a smooth wave though those 5 points
8. Extend graph through as many cycles in both directions
   as desired.

The rule is the same for the cosine graph of 



except for step 6, which is

6. Plot the 5 points:
   (S,A), (S+P/4,0), (S+P/2,-A), (S+3P/4,0), (S+P,A)

-------------------------------

Consider the following function 
 

First write it as



1. Compare graph to  and determine that
   A = 2, B = 1/4, C = 
2. Amplitude = 
3. Period = P = ÷ = ÷ = · = 
4. x-coordinate of starting point for basic cycle = S = ÷ 
   = ÷ = · =  
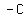5. Mark these five points on the x-axis:
   S, S+P/4, S+P/2, S+3P/4, S+P
   , , , , 

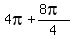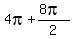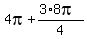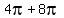   They simplify to:

   , , , , 

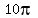 6. Plot the 5 points:
   (S,0), (S+P/4,A), (S+P/2,0), (S+3P/4,-A), (S+P,0)
   which are
   (4p,0), (6p,2), (8p,0), (10p,-2), (12p,0)
   and have numerical values for plotting:
   (12.6,0), (18.8,2), (25.1,0), (31.4,-2), (37.7,0) 

7. Draw a smooth wave though those 5 points



8. Extend graph through as many cycles in both directions
   as desired.



Edwin