(x - 3)5
The exponent is 5, so there will be 1 more term than the exponent. So there
will be 6 terms. The two terms in the binomial are x and -3. so write
" (x) (-3) " 6 times with + signs sandwiched in between, and leaving room for
an exponent and a coefficient for each term, like this:
(x) (-3) + (x) (-3) + (x) (-3) + (x) (-3) + (x) (-3) + (x) (-3)
Next fill in the exponents of the first term (x) descending from 5 to 0.
That is, write in exponents of (x) that start with 5 and go down to 0, i.e.,
5,4,3,2,1,0, like this:
(x)5(-3) + (x)4(-3) + (x)3(-3) + (x)2(-3) + (x)1(-3) + (x)0(-3)
Next fill in the exponents of the second term (-3) ascending from 0 to 5.
That is, write in exponents of (-3) that start with 0 and go up to 5, i.e.,
0,1,2,3,4,5, like this:
(x)5(-3)0 + (x)4(-3)1 + (x)3(-3)2 + (x)2(-3)3 + (x)1(-3)4 + (x)0(-3)5
Now we have everything except the coefficients and the simplification.
There are three methods for getting the 6 coefficients:
Method 1: Pascal's triangle:
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
So the coefficients of the 6 terms are 1, 5, 10, 10, 5, 1
Method 2: Calculate them by formula for combinations:
C(5,0) = 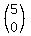 =
= 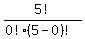 =
= 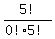 =
= 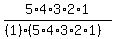 =
= 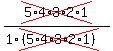 = 1
C(5,1) =
= 1
C(5,1) = 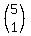 =
= 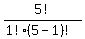 =
= 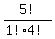 =
= 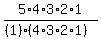 =
=  = 5
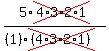
C(5,2) =
= 5
C(5,2) = 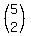 =
= 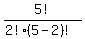 =
= 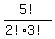 =
= 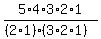 =
= 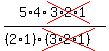 = 10
C(5,3) =
= 10
C(5,3) = 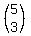 =
= 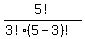 =
= 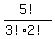 =
= 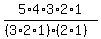 =
=  = 10
C(5,4) =
= 10
C(5,4) = 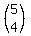 =
= 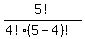 =
= 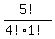 =
= 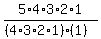 =
= 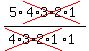 = 5
C(5,5) =
= 5
C(5,5) = 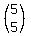 =
= 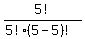 =
= 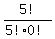 =
= 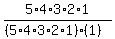 =
= 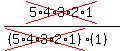 = 1
Methgod 3: Calculate them recursively:
Coefficient 1: Always 1, so we have
1(x)5(-3)0
Coefficient 2:
Take the previous coefficient, 1, multiply by the exponent of
the first term, x, get 1*5 or 5. divide by the number of term
which the previous term is, which is the 1st term so we divide
5 by 1 and get 5. So we have
1(x)5(-3)0 + 5(x)4(-3)1
Coefficient 3:
Take the previous coefficient, 5, multiply by the exponent of
the first term, x, get 5*4 or 20. divide by the number of term
which the previous term is, which is the 2nd term so we divide
20 by 2 and get 10. So we have
1(x)5(-3)0 + 5(x)4(-3)1 + 10(x)3(-3)2
Coefficient 4:
Take the previous coefficient, 10, multiply by the exponent of
the first term, x, get 10*3 or 30. divide by the number of term
which the previous term is, which is the 3rd term so we divide
30 by 3 and get 10. So we have
1(x)5(-3)0 + 5(x)4(-3)1 + 10(x)3(-3)2 + 10(x)2(-3)3
Coefficient 5:
Take the previous coefficient, 10, multiply by the exponent of
the first term, x, get 10*2 or 20. divide by the number of term
which the previous term is, which is the 4th term so we divide
20 by 4 and get 5. So we have
1(x)5(-3)0 + 5(x)4(-3)1 + 10(x)3(-3)2 + 10(x)2(-3)3 + 5(x)1(-3)4
Coefficient 6:
Take the previous coefficient, 5, multiply by the exponent of
the first term, x, get 5*1 or 5. divide by the number of term
which the previous term is, which is the 5th term so we divide
5 by 5 and get 1. So we have
1(x)5(-3)0 + 5(x)4(-3)1 + 10(x)3(-3)2 + 10(x)2(-3)3 + 5(x)1(-3)4 + 1(x)0(-3)5
So coefficients 1,5,10,10,5,1, are what you get regardless of which
of the three methods you use to get the coefficients. There is the
shortcut that the coefficients are symmetrical, so when you get
half-way through, you know what the rest are because they are just
like the first half.
Anyway,
1(x)5(-3)0 + 5(x)4(-3)1 + 10(x)3(-3)2 + 10(x)2(-3)3 + 5(x)1(-3)4 + 1(x)0(-3)5
simplifies to:
x5 - 15x4 + 903 - 2703 + 405x - 243
I assume you can do that.
Edwin
= 1
Methgod 3: Calculate them recursively:
Coefficient 1: Always 1, so we have
1(x)5(-3)0
Coefficient 2:
Take the previous coefficient, 1, multiply by the exponent of
the first term, x, get 1*5 or 5. divide by the number of term
which the previous term is, which is the 1st term so we divide
5 by 1 and get 5. So we have
1(x)5(-3)0 + 5(x)4(-3)1
Coefficient 3:
Take the previous coefficient, 5, multiply by the exponent of
the first term, x, get 5*4 or 20. divide by the number of term
which the previous term is, which is the 2nd term so we divide
20 by 2 and get 10. So we have
1(x)5(-3)0 + 5(x)4(-3)1 + 10(x)3(-3)2
Coefficient 4:
Take the previous coefficient, 10, multiply by the exponent of
the first term, x, get 10*3 or 30. divide by the number of term
which the previous term is, which is the 3rd term so we divide
30 by 3 and get 10. So we have
1(x)5(-3)0 + 5(x)4(-3)1 + 10(x)3(-3)2 + 10(x)2(-3)3
Coefficient 5:
Take the previous coefficient, 10, multiply by the exponent of
the first term, x, get 10*2 or 20. divide by the number of term
which the previous term is, which is the 4th term so we divide
20 by 4 and get 5. So we have
1(x)5(-3)0 + 5(x)4(-3)1 + 10(x)3(-3)2 + 10(x)2(-3)3 + 5(x)1(-3)4
Coefficient 6:
Take the previous coefficient, 5, multiply by the exponent of
the first term, x, get 5*1 or 5. divide by the number of term
which the previous term is, which is the 5th term so we divide
5 by 5 and get 1. So we have
1(x)5(-3)0 + 5(x)4(-3)1 + 10(x)3(-3)2 + 10(x)2(-3)3 + 5(x)1(-3)4 + 1(x)0(-3)5
So coefficients 1,5,10,10,5,1, are what you get regardless of which
of the three methods you use to get the coefficients. There is the
shortcut that the coefficients are symmetrical, so when you get
half-way through, you know what the rest are because they are just
like the first half.
Anyway,
1(x)5(-3)0 + 5(x)4(-3)1 + 10(x)3(-3)2 + 10(x)2(-3)3 + 5(x)1(-3)4 + 1(x)0(-3)5
simplifies to:
x5 - 15x4 + 903 - 2703 + 405x - 243
I assume you can do that.
Edwin