Question 753765: Form a polynomial f(x) with real coefficients having the given degree and zeros. Expand into standard form (do not leave it factored).
Degree: 3, Zeros: -5 and 6+i
Answer by josgarithmetic(39630)   (Show Source): (Show Source):
You can put this solution on YOUR website! You want three zeros and you're given one real and one complex with imaginary. This means you also include the conjugate for the complex root, so include also 6-i.
Your binomial factors for your function are  , , 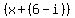 , and , and  . .
Just to be sure about the complex roots, for root R, binomial factor is (x-R) because when x=R, the binomial is 0.
If a zero is 6-i, then the binomial factor for it is (x-(-(6-i)))=(x-(-6+i))=x+6-i=(x+(6-i)).
If a zero is 6+i, then the binomial factor for it is (x-(-(6+i)))=(x-(-6-i))=x+6+i=(x+(6+i))
The complex with imaginary parts should be multiplied to get a product, or a quadratic factor for the original polynomial, for simpler writing. Find this:

So the function in factored form without showing any imaginary number is

I left the function in factored form (at least with no imaginaries), not quite the way you have asked in your question. You can finish multiplying this into GENERAL form if you want that.
|
|
|