SOLUTION: Without graphing, find the vertex and the maximum and minimum value of f(x) f(x)= -4/7(x-4)^2+8

Algebra ->  Graphs -> SOLUTION: Without graphing, find the vertex and the maximum and minimum value of f(x) f(x)= -4/7(x-4)^2+8      Log On


   

Question 753632: Without graphing, find the vertex and the maximum and minimum value of f(x)
f(x)= -4/7(x-4)^2+8
Answer by KMST(5328) About Me  (Show Source):
You can put this solution on YOUR website!
f%28x%29=+%28-4%2F7%29%28x-4%29%5E2%2B8 is a quadratic function, so its graph is a parabola.
f%28x%29=+%28-4%2F7%29%28x-4%29%5E2%2B8 is the equation of that parabola in vertex form.
The vertex form is the form that makes it easiest to find the vertex.
When x=4 x-4=0 and f%28x%29=+%28-4%2F7%29%28x-4%29%5E2%2B8=%28-4%2F7%290%5E2%2B8=8
For all other values of x,
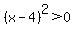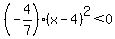%28x-4%29%5E2%3E0, %28-4%2F7%29%28x-4%29%5E2%3C0, and f%28x%29=+%28-4%2F7%29%28x-4%29%5E2%2B8%3C=8
No matter what value x takes, f%28x%29%3C=8
and f%28x%29=8 only when x=4.
The function has a maximum at x=4,
and the value of that maximum is f%284%29=8.
That corresponds to the vertex of the parabola, the point (4,8).
The function does not have a minimum; it can take any negative value you can think of.
The graph looks like this:
graph%28300%2C300%2C-6%2C14%2C-10%2C10%2C%28-4%2F7%29%28x-4%29%5E2%2B8%29
Parabolas can look like this graph%28100%2C100%2C1%2C7%2C3%2C9%2C%28-4%2F7%29%28x-4%29%5E2%2B8%29 or like this graph%28100%2C100%2C1%2C7%2C-9%2C-3%2C4%2F7%2A%28x-4%29%5E2-8%29
They can have a maximum or a minimum, but not both, and whichever they have happens at the vertex.