|
Question 752890: how do you write out an equation for a parabola with the vertex (0,0) and a focus (0, -1/12)?
i have tried to fit it in the equation (x-h)^2+(y-k)^2=r^2, but i got a completely off- answer...
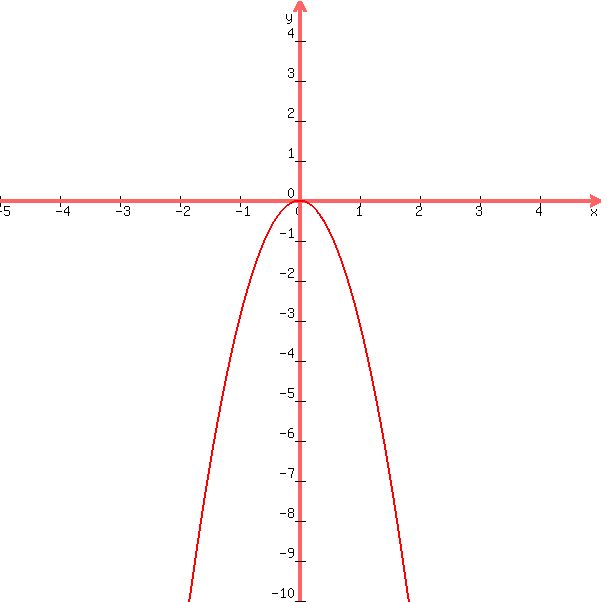
I looked up the answer key online, and it said that the answer is " y = -3x^2 " , but i am NOT getting even close..
Found 2 solutions by josgarithmetic, MathLover1:
Answer by josgarithmetic(39617)   (Show Source):
You can put this solution on YOUR website! The model you tried to fit did not work because that is a form of equation for a circle.
When you use the definition of a parabola to derive an equation, using a focal distance p from the vertex, you get a general equation  . This is a parabola with vertex on the origin, and vertex at a minimum. This derived equation can equivalently be written  . In your case, seeing the vertex is (0,0) and the focus is (0,-1/12), you should be able to know the value for p for the model. If you SEE this value for p, then good! Put in the values into  and simplify.
This should now be obvious. Vertex is (0,0) and focus (0,-1/12). p=1/12, and because the parabola opens DOWNWARD, the coefficient on x^2 must be LESS THAN ZERO, so you show a negative sign (instead of implying a positive sign).
Answer by MathLover1(20850)  (Show Source):
You can put this solution on YOUR website! given:
the vertex ( ,) and a focus (, )
The directed distance from the vertex to the focus is called  , the "parabolic constant". If going from vertex to focus is an upward or rightward motion, then  is positive. If downward or leftward, then  is negative. Here is negative, in fact,it is because going from the vertex (,) to the focus.
The value of is , since that is the directed distance from the vertex to the focus. Since the axis is vertical, the general equation is
So your equation is :
|
|
|
| |
