|
Question 751108: Classify the conic section:
1. x2 + y2 = 36
2. x2 - y2 = 36
3. 5x2 + 9y2 = 45
4. x2 + y2 = 121
5. y = 17
6. What is the standard equation of the circle with radius 4, and center (0,0)?
7. What is the standard equation of the circle with radius 5, and center (-5,-1)?
8. Name the center and radius of the circle whose equation is x2 + y2 = 49.
9. What are the vertices of the ellipse whose equation is (x2)/25 + (y2)/9 = 1?
10. What are the vertices of the ellipse whose equation is (x2)/9 + (y2)/36 = 1?
11. What is the center of the ellipse whose equation is (x2)/25 + (y2)/4 = 1?
12. What is the center of the ellipse whose equation is (x+1)2 / 4 + (y2)/1 = 1?
13. What is the center of the hyperbola whose equation is (x2) - (y2) = 1?
14. What is the center of the hyperbola whose equation is (x2)/4 - (y2)/9 = 1?
15. What is the center of the hyperbola whose equation is [(x+2)2 / 9] - [(y-2)2 / 16] = 1?
16. How does the graph of the hyperbola whose equation is (x2)/9 - (y2)/25 = 1 open?
17. How does the graph of the hyperbola whose equation is (y2)/4 - (x2)/9 = 1 open?
18. Classify the conic section of the equation x2 + 2x + y2 + 6y = 15.
19. Classify the conic section of the equation 4x2 + 9y2 - 8x - 18y - 19 = 0.
20. Classify the conic section of the equation 9x2 - 3 = 18x + 4y.
Answer by Edwin McCravy(20063)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Classify the conic section:
1. x² + y² = 36 <-- circle since x² and y² have the SAME COEFFICIENT, 1,
when on the same side of the equation.
2. x² - y² = 36 <-- hyperbola since x² and y² have coefficients with
OPPOSITE SIGNS when on the same side of the equation.
3. 5x² + 9y² = 45 <-- ellipse since x² and y² have different coefficients
with THE SAME SIGN when on the same side of the
equation.
4. x² + y² = 121 <-- circle since x² and y² have the SAME COEFFICIENT, 1,
when on the same side of the equation.
5. y = 17 <-- line because it has NO x² or y² terms.
6. What is the standard equation of the circle with radius 4, and center (0,0)?
Start woth
(x-h)²+(y-k)²=r² where (h,k) is the center and r is the radius
(x-0)²+(y-0)²=4²
x² + y² = 16
7. What is the standard equation of the circle with radius 5, and center (-5,-1)?
Start woth
(x-h)²+(y-k)²=r² where (h,k) is the center and r is the radius
(x-(-5))²+(y-(-1))²=5²
(x+5)² + (y+1)² = 25
8. Name the center and radius of the circle whose equation is x² + y² = 49.
The reverse of the other problems:
Write it as
(x-0)²+(y-0)²=7²
Compare that to
(x-h)²+(y-k)²=r²
So the center is (h,k) = (0,0,) and its radius is 7
9. What are the vertices of the ellipse whose equation is (x²)/25 + (y²)/9 = 1?
The ellipse that has equation
     Since a > b, and a is uder x, the ellipse looks like this
Since a > b, and a is uder x, the ellipse looks like this  has vertices (h+a,k) and (h-a,k). The center is (h,k)
Write your equation as
has vertices (h+a,k) and (h-a,k). The center is (h,k)
Write your equation as
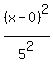  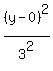   Then the vertices are (h+a,k) and (h-a,k) which are
(0+5,0) and (0-5,0)
(5,0) and (-5,0)
10. What are the vertices of the ellipse whose equation is (x²)/9 + (y²)/36 = 1?
The ellipse that has equation
Then the vertices are (h+a,k) and (h-a,k) which are
(0+5,0) and (0-5,0)
(5,0) and (-5,0)
10. What are the vertices of the ellipse whose equation is (x²)/9 + (y²)/36 = 1?
The ellipse that has equation
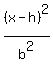  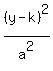   Since a > b, and a is under y, the ellipse looks like this
Since a > b, and a is under y, the ellipse looks like this  has vertices (h,k+a) and (h,k-a). The center is (h,k)
Write your equation as
has vertices (h,k+a) and (h,k-a). The center is (h,k)
Write your equation as
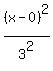  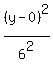   Then the vertices are (h,k+a) and (h,k-a) which are
(0,0+6) and (0,0-6)
(0,-6) and (0,6)
11. What is the center of the ellipse whose equation is (x²)/25 + (y²)/4 = 1?
Write it as
Then the vertices are (h,k+a) and (h,k-a) which are
(0,0+6) and (0,0-6)
(0,-6) and (0,6)
11. What is the center of the ellipse whose equation is (x²)/25 + (y²)/4 = 1?
Write it as
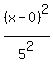  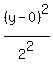   compare to
compare to
     So center = (h,k) = (0,0)
12. What is the center of the ellipse whose equation is (x+1)²/4 + (y²)/1 = 1?
The ellipse that has equation
So center = (h,k) = (0,0)
12. What is the center of the ellipse whose equation is (x+1)²/4 + (y²)/1 = 1?
The ellipse that has equation
     Since a > b, and a is under x, the ellipse looks like this
Since a > b, and a is under x, the ellipse looks like this  It has center is (h,k)
Write your equation as
It has center is (h,k)
Write your equation as
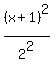  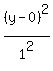   Compare it to
Compare it to
     and see x+1 = x-h and y-k = y-0
1 = -h -k = 0
-1 = h k = 0
So the center = (h,k) = (-1,0)
13. What is the center of the hyperbola whose equation is (x²) - (y²) = 1?
The hyperbola that has equation
and see x+1 = x-h and y-k = y-0
1 = -h -k = 0
-1 = h k = 0
So the center = (h,k) = (-1,0)
13. What is the center of the hyperbola whose equation is (x²) - (y²) = 1?
The hyperbola that has equation
     Since a is uder x, the hyperbola looks like this )(
It has has center is (h,k)
Write your equation as
Since a is uder x, the hyperbola looks like this )(
It has has center is (h,k)
Write your equation as
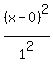  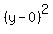   Compare to
Compare to
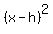  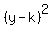   and h=0, k=0, so its center is (h,k) = (0,0)
14. What is the center of the hyperbola whose equation is (x²)/4 - (y²)/9 = 1?
The hyperbola that has equation
and h=0, k=0, so its center is (h,k) = (0,0)
14. What is the center of the hyperbola whose equation is (x²)/4 - (y²)/9 = 1?
The hyperbola that has equation
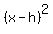  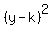   Since a is uder x, the hyperbola looks like this )(
It has has center is (h,k)
Write your equation as
Since a is uder x, the hyperbola looks like this )(
It has has center is (h,k)
Write your equation as
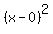  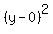   Compare to
Compare to
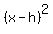  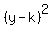   and h=0, k=0, so its center is (h,k) = (0,0)
15. What is the center of the hyperbola whose equation is [(x+2)²/9] - [(y-2)²/16] = 1?
The hyperbola that has equation
and h=0, k=0, so its center is (h,k) = (0,0)
15. What is the center of the hyperbola whose equation is [(x+2)²/9] - [(y-2)²/16] = 1?
The hyperbola that has equation
     Since a is under x, the hyperbola looks like this )(
It has has center is (h,k)
Write your equation as
Since a is under x, the hyperbola looks like this )(
It has has center is (h,k)
Write your equation as
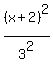  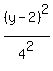   Compare to
Compare to
     x-h = x+2 y-k = y-2
-h = 2 -k = -2
h = -2 k = 2
So the center is (h,k) = (-2,2)
16. How does the graph of the hyperbola whose equation is (x²)/9 - (y²)/25 = 1 open?
The hyperbola that has equation
x-h = x+2 y-k = y-2
-h = 2 -k = -2
h = -2 k = 2
So the center is (h,k) = (-2,2)
16. How does the graph of the hyperbola whose equation is (x²)/9 - (y²)/25 = 1 open?
The hyperbola that has equation
     Since a is under x, the hyperbola looks like this )(,
so it opens right and left
17. How does the graph of the hyperbola whose equation is (y²)/4 - (x²)/9 = 1
open?
The hyperbola that has equation
Since a is under x, the hyperbola looks like this )(,
so it opens right and left
17. How does the graph of the hyperbola whose equation is (y²)/4 - (x²)/9 = 1
open?
The hyperbola that has equation
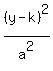  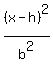   Since a is under y, the hyperbola looks like this
Since a is under y, the hyperbola looks like this  so it opens up and down.
18. Classify the conic section of the equation x² + 2x + y² + 6y = 15.
Circle since x² and y² have the SAME COEFFICIENT, 1, when on the same
side of the equation.
19. Classify the conic section of the equation 4x² + 9y² - 8x - 18y - 19 = 0.
Ellipse since x² and y² have different coefficients with THE SAME SIGNS when
on the same side of the equation.
20. Classify the conic section of the equation 9x² - 3 = 18x + 4y.
Parabola since there is only one term that has a variable squared.
Edwin
so it opens up and down.
18. Classify the conic section of the equation x² + 2x + y² + 6y = 15.
Circle since x² and y² have the SAME COEFFICIENT, 1, when on the same
side of the equation.
19. Classify the conic section of the equation 4x² + 9y² - 8x - 18y - 19 = 0.
Ellipse since x² and y² have different coefficients with THE SAME SIGNS when
on the same side of the equation.
20. Classify the conic section of the equation 9x² - 3 = 18x + 4y.
Parabola since there is only one term that has a variable squared.
Edwin
|
|
|
| |