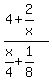 Write the
Write the  as
as  so everything
will be a fraction.
so everything
will be a fraction.
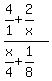 Then put parentheses around the top and the bottom:
Then put parentheses around the top and the bottom:
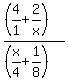 The four denominators are 1, x, 4, and 8
The LCD of those is 8x, so multiply by the
fraction
The four denominators are 1, x, 4, and 8
The LCD of those is 8x, so multiply by the
fraction 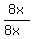 but write it as
but write it as
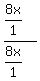 So now we have
So now we have
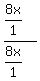 ·
·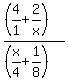 Now remove the parentheses by distributing on the
top and bottom:
Now remove the parentheses by distributing on the
top and bottom:
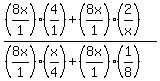 Cancel what will cancel and you have:
Cancel what will cancel and you have:
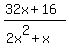 Now factor 16 out of the top and x out of the bottom:
Now factor 16 out of the top and x out of the bottom:
 Cancel the
Cancel the 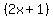 's and all that's left is
's and all that's left is
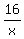 Edwin
Edwin