Question 750071: If 8 students are seated on each bench ,3 benches are left over .If 5 students are seated on each bench,12 students are left over How many benches students are there?
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! AS A SYSTEM OF EQUATIONS PROBLEM:
 = number of students = number of students
 = number of benches = number of benches
"If 5 students are seated on each bench, 12 students are left over" translates as

"If 8 students are seated on each bench, 3 benches are left over" cound be translated as
 if we are creative enough to think that the 3 empty benches could have housed if we are creative enough to think that the 3 empty benches could have housed  extra students. extra students.
Otherwise, we could translate "If 8 students are seated on each bench, 3 benches are left over" literally as
 since since 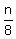 is the number of benches that are occupied. is the number of benches that are occupied.
Of course, the two equations are equivalent:
 --> -->  --> -->  --> --> 
 --> -->  --> -->  --> -->  --> -->  --> -->  --> --> 
AS A GUESS-AND-CHECK/DIVISIBILITY PROBLEM:
Since all students fit into a number  of benches with of benches with  students on each bench, the number of students students on each bench, the number of students 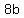 is a multiple of is a multiple of  . .
Sitting  students per bench you fill all the benches and have 12 students left over. students per bench you fill all the benches and have 12 students left over.
You could start guessing and checking from there, but it may be time consuming. You could have 4 or more benches, and 8, 16, 24, 32, 40, ... students. You can try each number, or skip some. Making a table can help. It would be better to reduce the number of choices to try.
Guessing away without further thought:
You could imagine having 4 benches. With 8 students, you can fill 1 bench with 8 students and would have 3 benches left. But with a total of 4 benches, sitting 5 on each bench you need  students to fill the benches and have 12 students left over. It must be more than 8 students. students to fill the benches and have 12 students left over. It must be more than 8 students.
With 5 benches, you can fill 2 benches with 8 students each (a total of 16 students), and would have 3 benches left. But 5 benches at 5 students per bench would sit 25 students, so you could not fill those 5 benches and have 12 students left over, so there are more than 5 benches and more than 16 students.
With 6 benches, you could fill 3 benches with 8 students each (24 student total), and would have 3 benches left. But 6 benches at 5 students per bench would sit 30 students, so 6 benches/24 students is still too low.
Let's skip 7 benches and go to 8 benches.
With 8 benches, you could fill 5 benches with 8 students each (40 students), and would have 3 benches left. But 8 benches at 5 students per bench would sit 40 students, with no student left over, so the numbers of benches/students at 8/40 are still too low.
Let's skip further and go to 13 benches.
With 13 benches/80 students, you could fill 10 benches with 8 students each and would have 3 benches left. But 31 benches at 5 students per bench would sit 65 students, with  students left over, and that is too many. students left over, and that is too many.
The numbers of benches/students are less than 13/80, so we may try the next smaller guess, 12 benches/72 students.
With 12 benches/72 students, you could fill 9 benches with 8 students each and would have 3 benches left. With 12 benches, at 5 students per bench, you would sit 60 students, with  students left over, and that is exactly what the problem asks for. So students left over, and that is exactly what the problem asks for. So  benches and benches and  students is the answer. students is the answer.
ALTERNATIVELY, you can use the information to reduce the number of guesses to try to 4 benches/32 students, 12 benches/72 students, 4 benches/32 students, 20 benches/112 students, etc.
One way:
Sitting  students per bench you fill all the benches and have 12 students left.T hat means you could fill students per bench you fill all the benches and have 12 students left.T hat means you could fill  more benches with another more benches with another  students and have just students and have just  students without a seat. students without a seat.
That tells you that the number of students is  more than a multiple of more than a multiple of  . The multiples of 5 that are not odd rather than even (like 5,15, 15, 35, etc) would not work, because adding . The multiples of 5 that are not odd rather than even (like 5,15, 15, 35, etc) would not work, because adding  to those numbers will still give you and odd number for the total number of students, and the total number of students is a multiple of 8, so it must be even. to those numbers will still give you and odd number for the total number of students, and the total number of students is a multiple of 8, so it must be even.
Now we know that the total number of students should be an even multiple of 5 (a multiple of 10) plus 2, and it must also be a multiple of 8.
The total number of students cannot be 12, or 22, or 42, or 52, or 62, or 82, or 92, or 102, or 122 (not multiples of 8), but we should try 32, 72, and 112.
A craftier way (maybe too creative) to get at the same point:
If I gave you 8 more students, and 4 more benches you could have everyone comfortably seated at 5 students per bench.
With the 8 added students, the number of students would be a multiple of 8 and a multiple of 5, so it would be a multiple of 40.
The number of benches would be a multiple of 8 and the number of students would be a multiple of 40, as in 8/40, 16/80, 24,120.
That means that before being given the 4 extra benches/8 extra students you had
 benches/ benches/ students, or students, or
 benches/ benches/ students, or students, or
 benches/ benches/ students, or ... students, or ...
At 8 students per bench,
32 students use  benches, using all 4 benches with no bench left over (too few); and benches, using all 4 benches with no bench left over (too few); and
112 students use  benches, with benches, with  benches left over (too many); and benches left over (too many); and
72 students use  benches, with benches, with  benches left over (just right). benches left over (just right).
|
|
|