Question 749494: consider the curve y=2logx, where log is the natural logarithm. let α be the tangent to that curve which passes through the origin, let P be the point of contact of α and that curve, and let m be the straight line perpendicular to the tangent α at P. We are to find the equations of the straight lines α and m and the area S of the region bounded by the curve y=2logx, the straight line m, and the x-axis
let t be the x-coordinate of the poin P, then t satisfies log t=(A). Hence the equation of α is

the equation of m is

thus the area S of the region is

solve for A,B,C,D,E,F and G
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! The function is 
Its graph crosses the x-axis at the point where 
 --> -->  --> -->  --> --> 
The x-coordinate of point P is  . .
The slope of the tangent at point P is the value of the derivative at that point.
y'=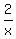 , so the slope of the tangent at , so the slope of the tangent at  is is  . .
Since the line  tangent at P passes through the origin, its equation must be tangent at P passes through the origin, its equation must be

At point P, with  , ,  --> --> 
Since point P is on the graph of  , its y-coordinate is , its y-coordinate is 
So  --> -->  --> -->  --> -->  and P is (e,2). and P is (e,2).
Now we can find the equation of  : :
 --> -->  --> -->  is is 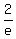 , ,
line  perpendicular to perpendicular to  must have a slope of must have a slope of  . .
As  passes through P(e,2) its equation is passes through P(e,2) its equation is
 --> -->  --> -->  --> --> 
So  , ,  , and , and 
The line  crosses the x-axis at the point where crosses the x-axis at the point where 
 --> -->  --> -->  --> -->  --> -->  --> --> 
The area  of the region bounded by the curve of the region bounded by the curve  , the straight line , the straight line  , and the x-axis is shown below. , and the x-axis is shown below.

 can be can be calculated as the sum of: can be can be calculated as the sum of:
the area below  , and above the x-axis, between , and above the x-axis, between  and and  , , 
plus the area below  between between  and and  , , 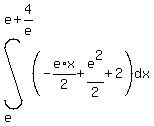
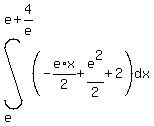 is easier than it seems. is easier than it seems.
It's just the area of the triangle with vertices (e,0), P(e,2), and (e+e/4,0)
Its base is 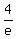 ; its height is ; its height is  , and its area is , and its area is  . .
Since  , ,

So  and and 
|
|
|