SOLUTION: let α be a real number, let us translate the graph of the cubic function {{{y=f(x)=x^3+ alpha}}}{{{x^2 + bx +c }}} .....{1) so that the point (α,f(α)) on the graph

Algebra ->  Quadratic Equations and Parabolas -> SOLUTION: let α be a real number, let us translate the graph of the cubic function {{{y=f(x)=x^3+ alpha}}}{{{x^2 + bx +c }}} .....{1) so that the point (α,f(α)) on the graph      Log On


   

Question 749493: let α be a real number, let us translate the graph of the cubic function
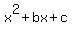y=f%28x%29=x%5E3%2B+alphax%5E2+%2B+bx+%2Bc+ .....{1)
so that the point (α,f(α)) on the graph (1) is translated into the origin (0,0), and express the function of the translated graph in terms of f'(α) and f"(α)
next we consder the translation which translates the point (α,f(α)) on the graph of (1) into the origin, we replace x with x+α and y with y+f(α) in (1), and obtain the expression y=x^3+ f"(α).x^2/A + f'(α)x
As an example, consider the function
f%28x%29=x%5E3+-12x%5E2+%2B48x+-68....(2)
f'(4)=0 and f"(4)=0
we see that when we translate the graph of (2) so that the point (B,C) on the graph is moved to the origin, we get the graph of y=x%5E3
solve for [A] [B] and [C]
Answer by KMST(5328) About Me  (Show Source):
You can put this solution on YOUR website!
This problem was posted as problem # 749493 (2013-05-16 12:20:44) and as problem # 750070 (2013-05-18 05:10:05). Each time something is was being lost in translation, but it helped to be able to listen to the message twice.

One way to translate a graph so that point (a, f(a)) moves to the origin, point (0, 0), is to replace 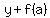y with y%2Bf%28a%29 and x with x%2Ba and then solve for y
When we do that to
y=f%28x%29=x%5E3+%2B+alpha%2Ax%5E2%2Bbx%2Bc we get



y=x%5E3%2B3ax%5E2%2B3a%5E2x%2Balpha%2Ax%5E2%2Balpha%2A2ax%2Bbx
y=x%5E3%2B%283a%2Balpha%29x%5E2%2B%283a%5E2%2B2alpha%2Aa%2Bb%29x
The first and second derivatives of f%28x%29=x%5E3+%2B+alpha%2Ax%5E2%2Bbx%2Bc are
%22f%27%28x%29%22=3x%5E2%2B2alpha%2Ax%2Bb and %22f%27%27%28x%29%22=6x%2B2alpha=2%283x%2Balpha%29 so
%22f%27%28a%29%22=3a%5E2%2B2alpha%2Aa%2Bb and %22f%27%27%28a%29%22=6a%2B2alpha=2%283a%2Balpha%29
Comparing to y=x%5E3%2B%283a%2Balpha%29x%5E2%2B%283a%5E2%2B2alpha%2Aa%2Bb%29x we see that the coefficient of x is indeed %22f%27%28a%29%22=3a%5E2%2B2alpha%2Aa%2Bb
and %22f%27%27%28a%29%22%2F2=2%283a%2Balpha%29%2F2=3a%2Balphais the coefficient of x%5E2
so y=x%5E3%2B%28%22f%27%27%28a%29%22%2F2%29x%5E2%2B%22f%27%28a%29%22%2Ax and highlight%28A=2%29

How would I use all of the above to find the coordinates of the point (B, C) in the graph of
y=x%5E3-12x%5E2%2B48x-68 that when translated to the origin turns the function into y=x%5E3?

I wouldn't.

I would realize that %28x-4%29%5E3=x%5E3-12x%5E2%2B48x-64 and that y=%28x-4%29%5E3-4
which is y=x%5E3 translated 4 units to the left and 4 units down,
and that is the translation that would bring point (B, C) = (4, 4) to (0, 0).
That looks to me like the most efficient way to the solution.

Or maybe after being told that
f%28x%29=x%5E3-12x%5E2%2B48x-68 translated turns into y=x%5E3 and that
%22f%27%27%284%29%22=0
I would realize that f%28x%29=x%5E3-12x%5E2%2B48x-68 must have just one inflection point, just like y=x%5E2.
Since I know that y=x%5E2 has its inflection point at (0, 0),
I would realize that the inflection point of f%28x%29 at x=4 must be the point translated to the origin.
Then I would know that B=4 and would only need to calculate the y-coordinate of the inflection point, C=f%284%29
C=4%5E3-12%2A4%5E2%2B48%2A4-68 --> C=64-12%2A16%2B192-68 --> C=64-192%2B192-68 --> C=64-68 --> C=-4

But maybe we are supposed to use the first part and realize that with a=4 it would man that translating (4, f(4)) into the origin would transform
f%28x%29=x%5E3-12x%5E2%2B48x-68 into y=x%5E3%2B%28%22f%27%27%28a%29%22%2F2%29x%5E2%2B%22f%27%28a%29%22%2Ax
and if %22f%27%284%29%22=0 and %22f%27%27%284%29%22=0 the equation
y=x%5E3%2B%28%22f%27%27%28a%29%22%2F2%29x%5E2%2B%22f%27%28a%29%22%2Ax transforms into y=x%5E3