SOLUTION: [log(x-4)=1-log(x-1)] + [the distance between (2,-3) and (-8, -3+ square root of 21)] I tried solving the distance part and got 14.6, but I think its wrong. I have no idea whe

Algebra ->  Logarithm Solvers, Trainers and Word Problems -> SOLUTION: [log(x-4)=1-log(x-1)] + [the distance between (2,-3) and (-8, -3+ square root of 21)] I tried solving the distance part and got 14.6, but I think its wrong. I have no idea whe      Log On


   

Question 749489: [log(x-4)=1-log(x-1)] + [the distance between (2,-3) and (-8, -3+ square root of 21)]

I tried solving the distance part and got 14.6, but I think its wrong. I have no idea where to begin with the log part.
Answer by KMST(5328) About Me  (Show Source):
You can put this solution on YOUR website!
This diagram below shows points (2,-3) and (-8, -3%2Bsqrt%2821%29) circled, and the distance d between them


The distance between points (2,-3) and (-8, -3%2Bsqrt%2821%29
can be calculated as d=sqrt%28%28DELTA%28x%29%29%5E2%2B%28DELTA%28y%29%29%5E2%29
where DELTA%28x%29=abs%28-8-2%29=abs%28-10%29=10 is the difference between the x-coordinates of the points,
and DELTA%28y%29=abs%28-3%2Bsqrt%2821%29-%28-3%29%29=sqrt%2821%29 is the difference between the y-coordinates of the points.
It is not a difficult calculation, and no complicated distance formula needs to be memorized. (If your teacher disagrees, and requires that you
d=sqrt%2810%5E2%2B21%29=sqrt%28121%29=11
It is not a difficult calculation, and no complicated distance formula needs to be memorized. You do not even have to worry about the absolute values or the order of the numbers you subtract to get those differences because after you square them, it does not matter if it was -8-2=-10 and -2-%28-8%29=10; you get the same squared difference.

NOTE: If your teacher disagrees, and requires that you make it look complicated, you may have to write something like
d=sqrt%28%28x%5BB%5D-x%5BA%5D%29%5E2%2B%28y%5BB%5D-y%5BA%5D%29%5E2%29


After finding that distance, the problem log(x-4)=1-log(x-1) + [the distance between (2,-3) and (-8, -3+ square root of 21)]
turns into log%28x-4%29=1-log%28x-1%29%2B11
log%28x-4%29=1-log%28x-1%29%2B11 --> log%28x-4%29%2Blog%28x-1%29=1%2B11 --> log%28%28x-4%29%28x-1%29%29=12 --> %28x-4%29%28x-1%29=10%5E12 --> x%5E2-5x%2B4=10%5E12
The equation x%5E2-5x%2B4=10%5E12 --> x%5E2-5x%2B4-10%5E12=0 --> x%5E2-5x-999999999996=0 makes me suspect some typo in the problem.

IF it had been log(x-4)=-10-log(x-1) + [the distance between (2,-3) and (-8, -3+ square root of 21)] ,
it would simplify to
log%28x-4%29=-10-log%28x-1%29%2B11 --> log%28x-4%29%2Blog%28x-1%29=-10%2B11 --> log%28%28x-4%29%28x-1%29%29=1 --> %28x-4%29%28x-1%29=10%5E1 --> x%5E2-5x%2B4=10 --> x%5E2-5x%2B4-10=0 --> x%5E2-5x-6=0
with solutions x=-1 and x=6, and verifying in the original equation we would see that
x=6 is a solution of log%28x-4%29=-10-log%28x-1%29%2B11,
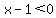but x=-1 does not work because it makes x-1%3C0 and x-4%3C0 and their logarithms would not exist.