|
Question 74942This question is from textbook Alegbra & Trig w/Geometry
: Find the solution to the equation: 6x – 3 = –2x + 21.
Find the solutions to the equation: x2 + 2x – 8 = 0.
Find the solutions to the equation: x-5/x = 4.
Solve the inequality 21/15-3x<0, and express the solution as an interval.
This question is from textbook Alegbra & Trig w/Geometry
Answer by funmath(2933)   (Show Source): (Show Source):
You can put this solution on YOUR website! Find the solution to the equation: 6x – 3 = –2x + 21.
6x+2x-3=-2x+2x+21
8x-3=21
8x-3+3=21+3
8x=24
8x/8=24/8

Check by letting x=3 and see if both sides equal.
6(3)-3=-2(3)+21
18-3=-6+21
15=15 We're right!!!!
:
Find the solutions to the equation: x2 + 2x – 8 = 0.
Factor:
x^2+2x-8=0
(x___)(x___)=0
Fill the blanks with two numbers that multiply to give you -8, but add to give you 2. 4*-2=-8 and 4-2=2
(x+4)(x-2)=0 Set each parentheses equal to 0 and solve for x.
x+4=0 or x-2=0
x+4-4=0-4 or x-2+2=0+2
 or or 
Once again, you can check your solutions by subtituting into the original equation and see if you get 0.
(-4)^2+2(-4)-8=0
16-8-8=0
0=0 This one's right.
(2)^2+2(2)-8=0
4+4-8=0
0=0 We're right again!!!
:
:
Find the solutions to the equation: x-5/x = 4.
I'm not sure where your fraction begins and ends. I'm going with the way that you typed it.
 x is the LCD, multiply everything by x. x is the LCD, multiply everything by x.

 Set the problem = to 0. Set the problem = to 0.

 Factor Factor
(x___)(x___)=0
Fill the blanks with two numbers that multiply to give you -5, but add to give you -4. -5*1=-5 and -5+1=-4
(x-5)(x+1)=0 set each factor =0 and solve for x
x-5=0 or x+1=0
x-5+5=0+5 or x+1-1=0-1
 or or 
Check by substitution:


 we're right on this one. we're right on this one.


 We're right again!!!! We're right again!!!!
Solve the inequality 21/15-3x<0, and express the solution as an interval.
This one is another one that I'm not sure about where your fraction's denominator begins or ends. I'm going with the way you typed it. If the -3x is part of the denominator let me know.
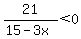
Let the denominator =0 to find the critical number.
15-3x=0
-15+15-3x=0-15
-3x=-15
-3x/-3=-15/-3
x=5
The intervals to test are (-infinity,5) and (5,infinity)
For the interval (-infinity,5), test x=0.
If x=0

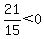 Not true Not true
For the interval (5,infinity), let x=5


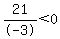
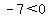 True True
Therefore, the solution is: (5,infinity)
Happy Calculating!!!!
|
|
|
| |