Question 74918: I am a very frustrated mother trying to help my son pass algebra. You have helped before with great success. I have 3 problems I am trying to help him with. If you would be so kind as to help.
1) A wallet contains four $5 bills, two $10 bills, and eight $1 bills.
A) If two bills are selected with the first bill being replaced. Find P ($5 and $5)
B)If two bills are selected WITHOUT the first bill being replaced Find P ($10 and $1)
2) A blue die and red die are rolled. Find the probability that an odd number is rolled on the blue die and a multiple of 3 rolled on the red die.
3) How many ways can you make a four digit combination if:the digits can be repeated (HInt 0 is also a digit)
P.S. Do you do one-on-one online tutoring or know someone who does?
Thank You
Mother trying to help her son
Answer by jim_thompson5910(35256)   (Show Source): (Show Source):
You can put this solution on YOUR website! 1)
A) The probability of selecting one $5 bill is the number of $5 bills out of the total number of bills. So you have 4 $5 bills out of a total of 14. So this looks like:

So the probability of getting two 5's are
 remember "and" means multiply the probabilities remember "and" means multiply the probabilities
So the chances of drawing 2 5's with the first one replaced is 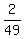 or 4% or 4%
B)If you don't replace the bill taken out, then the total decreases by 1 for the 2nd probability

So the chances of drawing 2 5's without the first one replaced is  or 4.3% or 4.3%
2)On a six-sided die there are 3 odd numbers out of 6 numbers. So the probability of rolling an odd number for the blue die is:

Since there are 2 numbers that are a multiple of 3 (3 and 6),the probability of rolling a multiple of 3 is:

So the probability of these events occurring together are:

It turns out that there is only one number that meets this condition. The number 3 is a multiple of 3 and is odd. Since the number 3 occurs once out of 6 numbers , the odds of rolling a 3 is 1/6, which justifies our answer.
3)For the 1st digit you have the numbers 0-9 to choose from. So you have 10 numbers to choose from for the 1st digit. For the 2nd digit its the same, since you can repeat the digits. This is the same for all of the digits, so you get

So there are a total of 10,000 combinations. It's easier to visualize this with a smaller set. Say we have 2 digits with only 0 and 1 as possible numbers, we would get this:
00,01,10,11
You can see there are 4 possible combinations. Since there are 2 numbers for both digits we can say

Which is our number of possible combinations. I hope that clears up things a bit. Currently I'm tutoring one-on-one for free. So feel free to send me any more problems or ask any more questions.
|
|
|