|
Question 748931: I Know That Some Are Not In The Category But Please Answer.. It Is So HARD.
1. Joseph can paint a house in 10 days, and George can paint the house in 12 days. How long will it take to paint the house if both work for five days, and then Joseph finishes the work?
2. Garry is one year more than twice as old as Badong. The two boys together are ten years older than Narva. If Narva is 3 years younger than Garry. Find Narva’s age.
3. The average of three numbers is 10. The second is one more than twice the first, and the third is 5 more than three times the first. Find these numbers.
4. Brine solution A is 5% salt while Brine B is 15%. How many liters of each should be mixed to get a 10 liters mixture that is 12% pure?
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! 1. If Joseph can paint a house in 10 days, Joseph can paint  of the house per day (that's his rate/speed of work). of the house per day (that's his rate/speed of work).
If George can paint the house in 12 days, George can paint  of the house per day. of the house per day.
(Joseph paints a little faster than George).
During the 5 days that both work together,
Joseph will paint  of the house, and of the house, and
George will paint  of the house. of the house.
Between the two of them, they almost have it finished in 5 days.
The fraction of the house painted during those 5 days is

The fraction of the house left to be painted is

That is the amount of work that George could do in 1 day.
Joseph, who is a little faster and could paint  finishes the work in a little less than one day and gets to go home a little earlier after finishing the job the 6th day. (or maybe he will use the time to clean up his brushes and put away all materials and equipment). finishes the work in a little less than one day and gets to go home a little earlier after finishing the job the 6th day. (or maybe he will use the time to clean up his brushes and put away all materials and equipment).
2. Let's name variables.
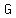 = Garry's age (in years) = Garry's age (in years)
 = Badong's age (in years) = Badong's age (in years)
 = Narva’s age (in years) = Narva’s age (in years)
Each sentence of the information given will translate into an equation and we will end up with a system of equations to solve, finding values for 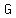 , ,  and and  . .
If Garry is one year more than twice as old as Badong, Garry's age is
 (1 year more than twice B) (1 year more than twice B)
If the Garry and Badong together are ten years older than Narva,

Narva is 3 years younger than Garry translates as

The 3 equations together form the system of equations

Systems of equations are solved by changing one equation at a time.
You can combine 2 equations to make a more convenient equation that can replace one of the 2 equations you combined.
You do not need to write as much as I did, but you have to keep track of what direction you are going so you do not go around in circles.
We start by substituting  for for 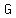
 --> -->  --> -->  --> -->  --> -->  --> -->  --> -->  --> --> 
3. Let's name variables.
 = the first number = the first number
 = the second number = the second number
 = the third number = the third number
The average of three numbers is 10 translates as
 --> --> 
The second (number) is one more than twice the first translates as

The third (number) is 5 more than three times the first translates as

That gives you an easy system 
Substituting into the first equation the expressions for  and and  given in the second and third equation, we get given in the second and third equation, we get
 --> -->  --> -->  --> --> 
 --> -->  --> -->  --> --> 
4. Let's name variables.
 = liters of solution A needed = liters of solution A needed
 = liters of solution B needed = liters of solution B needed
To get 10 liters of mixture we need to make  <--> <--> 
That could be one equation in a system of equations, or we could decide to use
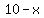 = liters of solution B needed = liters of solution B needed
and have just one variable all along.
Since brine solution A is 5% salt,  liters of it will contain an amount of salt equal to liters of it will contain an amount of salt equal to
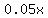
Since brine solution B is 15% salt, 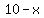 liters of it will contain an amount of salt equal to liters of it will contain an amount of salt equal to

The total amount of salt in the mix will be

which must equal 12% of 10 liters or 
So  --> -->  --> -->  --> -->  --> --> 
So you need  liters of solution A and liters of solution A and  liters of solution B. liters of solution B.
NOTE:
Notice that I did not give you units for the amount of salt.
I did not because the problem does not deserve it.
If it made a little more sense I would have said the amounts were in kilograms, but I would have to explain it as a chemical engineering mass balance problem.
To a chemist/chemical engineer (like me) this problem is total nonsense for at least 2 reasons:
1) mixing 3 liters of one solution with 7 liters of another do not necessarily give you 10 liters, and
2) concentrations should be clearly specified as in 5% w/v, where w/v means weight (w) in volume (v), meaning 5 kilograms of salt per 100 liters of brine solution (or 5 grams in 100 milliliters). If brine solution A was specified as 5% w/w (5 kilogram salt per
|
|
|
| |