Question 747785: A square is divided into three equal area by two parpllel lines drawn from opposite vertices.Determine the square in cm square if the distance between the two lines is 1 cm ?
Found 3 solutions by lynnlo, ikleyn, greenestamps:
Answer by lynnlo(4176)   (Show Source):
Answer by ikleyn(53475)  (Show Source):
You can put this solution on YOUR website! .
A square is divided into three equal areas by two parallel lines drawn from opposite vertices.
Determine the  of the square in cm square if the distance between the two lines is 1 cm
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Notice that I corrected/edited your post, to make
the problem's formulation correct from a Math point of view.
Make a plot following my description.
Let ABCD be our square with the side length 'x', so A, B, C and D are its vertices.
The lines divide our square into three equal areas, so the area of each part is  .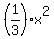
Draw the line AE from A to the side BC, so the intersection point E with BC
divides side BC in proportion BE:CE = 2:1.
In other words, B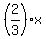E =  , XE =  .
Draw the line CF from the opposite vertex C to the side AD, so the intersection point F with AD
divides side AD in proportion DF:AF = 2:1.
In other words, D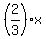F = , AF = .
So, now we have two right-angled triangles ABE and CDF of the area 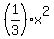 each,
and parallelogram AECF, whose area is also 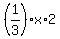 , since it is the remaining area.
So, now we have exactly the configuration described in the problem.
We can easy find the lengths of intervals AE and CF as hypotenuses of triangles ABE and CFD
AE = CF =  =  =  .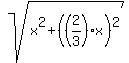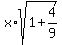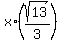
Now the area of the parallelogram AECF is, from one hand side, ,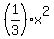
and from other hand side it is the product of its base AE by the height, which is 1 cm.
So, we can write this equation for the area of parallelogram AECF
=  .
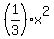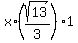Cancel common factors, and you will get
x = 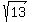 cm.
Hence, the area of the square ABCD is  = 13 cm^2. <<<---=== ANSWER
At this point, the problem is solved completely.
Answer by greenestamps(13261)  (Show Source):
You can put this solution on YOUR website!
Drawing the figure as described, we see the square divided into two congruent right triangles and a parallelogram, with all three figures having the same area.
Let x be the side length of the square.
The area of each right triangle is one-third the total area of the square,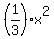
The length of one leg of the triangle is x; the length of the other leg is such that the area of the triangle -- one-half the product of the lengths of the two legs -- is 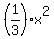. That makes the length of the other leg
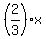
With legs of lengths  and 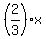, the length of the hypotenuse, from the Pythagorean Theorem, is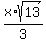 
Drawing an altitude of length 1 of the parallelogram produces a right triangle, similar to the two large triangles, with long leg of length 1 and hypotenuse of length  .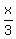
Using corresponding parts of similar triangles, we then have
The side length of the square in centimeters is  , so the area of the square in square centimeters is 13.
ANSWER: 13
|
|
|
