Question 746943: How do you work out x^2 + y^2 = 25; (3, -4)
I am doing practice for my math 3 class.
"Equation of Tangent Line to Circle"
I have been having problems with this problem because for my
Mtan part I don't know if a my answer is right.
I got Mtan= -3/4 I just need help to find if this is correct
And if the slope is negative or positive.
Found 2 solutions by Alan3354, MathTherapy:
Answer by Alan3354(69443)   (Show Source): (Show Source):
You can put this solution on YOUR website! I am doing practice for my math 3 class.
"Equation of Tangent Line to Circle"
I have been having problems with this problem because for my
Mtan part I don't know if a my answer is right.
I got Mtan= -3/4 I just need help to find if this is correct
And if the slope is negative or positive.
------------------
The slope of the tangent at any point on a circle centered at the origin is
m = -x/y
m = +3/4 at point (3,-4)
Answer by MathTherapy(10556)   (Show Source): (Show Source):
You can put this solution on YOUR website!
How do you work out x^2 + y^2 = 25; (3, -4)
I am doing practice for my math 3 class.
"Equation of Tangent Line to Circle"
I have been having problems with this problem because for my
Mtan part I don't know if a my answer is right.
I got Mtan= -3/4 I just need help to find if this is correct
And if the slope is negative or positive.
The coordinate point (3, - 4) is a solution to the equation:  . This coordinate point is also where the tangent line to the circle and the radius of the circle intersect. . This coordinate point is also where the tangent line to the circle and the radius of the circle intersect.
Looking at the equation,  , it can be seen that the coordinate point of the center of the circle is at (0, 0), or the origin. , it can be seen that the coordinate point of the center of the circle is at (0, 0), or the origin.
Now, since we have two coordinate points for the radius: (0, 0), and (3, - 4), we can see that the slope of the radius = 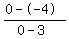 , or , or  , or , or 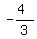
Since the slope of the radius of the circle is 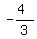 , and the radius is PERPENDICULAR to the tangent line, then the slope of the tangent line will be the negative reciprocal of the slope of the radius line, or , and the radius is PERPENDICULAR to the tangent line, then the slope of the tangent line will be the negative reciprocal of the slope of the radius line, or 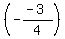 ------- ------- 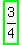
|
|
|