>>...pipe A can fill the pool in 8 hours...<<
Therefore pipe A can fill 1 pool in 8 hours. Therefore
A's pool-filling rate is 1 pool per 8 hours, which can be
written as 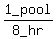 or
or 
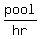 .
Suppose pipe B can fill the pool in x hours.
Then pipe B can fill 1 pool in x hours. Therefore
B's pool-filling rate is 1 pool per x hours, which can be
written as
.
Suppose pipe B can fill the pool in x hours.
Then pipe B can fill 1 pool in x hours. Therefore
B's pool-filling rate is 1 pool per x hours, which can be
written as 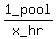 or
or 
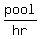 .
Suppose pipe C can fill the pool in y hours.
Then pipe C can fill 1 pool in y hours. Therefore
C's pool-filling rate is 1 pool per y hours, which can be
written as
.
Suppose pipe C can fill the pool in y hours.
Then pipe C can fill 1 pool in y hours. Therefore
C's pool-filling rate is 1 pool per y hours, which can be
written as 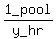 or
or 
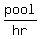 .
.
>>...pipes A and C can fill the pool in 6 hours...<<
So A and C's combined pool-filling rate is 1 pool per 6 hours,
which can be written as  or
or 
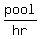 .
Now we use the fact that A and C's combined pool-filling rate
is the sum of their individual pool-filling rates to get this
equation:
.
Now we use the fact that A and C's combined pool-filling rate
is the sum of their individual pool-filling rates to get this
equation:
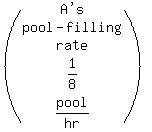

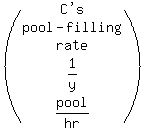

 So
So




 Above we have C's pool-filling rate as
Above we have C's pool-filling rate as 
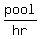 ,
so we solve that for
,
so we solve that for 







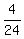




 so C's pool-filling rate is
so C's pool-filling rate is 
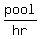 ,
,
>>...pipes B and C can fill the pool in 10 hours...<<
So B and C's combined pool-filling rate is 1 pool per 10 hours,
which can be written as 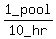 or
or 
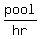 .
Now we use the fact that B and C's combined pool-filling rate
is the sum of their individual pool-filling rates to get this
equation:
.
Now we use the fact that B and C's combined pool-filling rate
is the sum of their individual pool-filling rates to get this
equation:
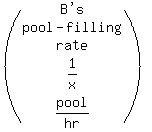

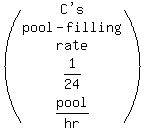

 So
So




 Above we have B's pool-filling rate as
Above we have B's pool-filling rate as 
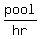 ,
so we solve that for
,
so we solve that for 







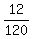




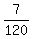 so B's pool-filling rate is
so B's pool-filling rate is 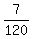
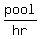 .
.
>>...How long will it take to fill the pool if all three pipes are used together?...<<
Suppose all three pipes can fill the pool in z hours.
So the combined pool-filling rate of all three is 1 pool per z hours,
which can be written as 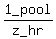 or
or 
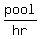 .
Then the equation comes from
.
Then the equation comes from
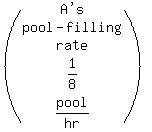

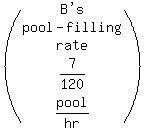

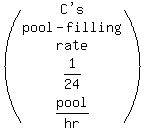




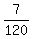



 Multiply through by LCD = 120z
15z + 7z + 5z = 120
27z = 120
z =
Multiply through by LCD = 120z
15z + 7z + 5z = 120
27z = 120
z = 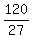 z =
z =  or
or 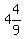 hour
or 4 hours, 26 minutes, 40 seconds.
Edwin
hour
or 4 hours, 26 minutes, 40 seconds.
Edwin