SOLUTION: I am trying to prove the following identity by induction (basic number theory course): 1^2 + 2^2 + ... + k^2 = (n*(n+1)*(2*n + 1))/6 So far I have that when n = 1, LHS = 1^2, R

Algebra ->  Equations -> SOLUTION: I am trying to prove the following identity by induction (basic number theory course): 1^2 + 2^2 + ... + k^2 = (n*(n+1)*(2*n + 1))/6 So far I have that when n = 1, LHS = 1^2, R      Log On


   

Question 7468: I am trying to prove the following identity by induction (basic number theory course):
1^2 + 2^2 + ... + k^2 = (n*(n+1)*(2*n + 1))/6
So far I have that when n = 1, LHS = 1^2, RHS = (1*2*3)/6 = 6/6 = 1
therefore the theory is true when n = 1
Assume it is true for some positive integer k
1^2 + 2^2 + ... + k^2 = (k*(k+1)*((2*k)+1))/6
then try to prove it is also true for k+1
1^2 + 2^2 + ... + k^2 + (k+1)^2 = ((k*(k+1)*((2*k)+1))/6) + (k+1)^2
I can rearrange this to give me (1/6*(k+1)* k*((2*k)+1)) + (k+1)^2
and I can factor (k+1)^2 to give me k^2 + 2k + 1 but I'm not sure I'm making any progress.
I found a solution that shows the next step is
(1/6*(k+1) * (k*((2*k)+1) + (6*(k+1)))
but I can't figure how to get there from where I am.
Any help would be greatly appreciated.
Answer by longjonsilver(2297) About Me  (Show Source):
You can put this solution on YOUR website!
i think some of your working is wrong.

Anyway, what i would do is the following:

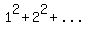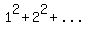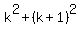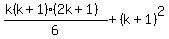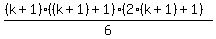
assuming that 1%5E2+%2B+2%5E2+%2B+... + k%5E2+=+%28k%28k%2B1%29%282k%2B1%29%29%2F6 then we have to prove that 1%5E2+%2B+2%5E2+%2B+... + k%5E2+%2B+%28k%2B1%29%5E2, which is %28k%28k%2B1%29%282k%2B1%29%29%2F6+%2B+%28k%2B1%29%5E2 will be equivalent to %28%28k%2B1%29%28%28k%2B1%29%2B1%29%282%28k%2B1%29%2B1%29%29%2F6

Is this OK?

Right... 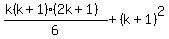%28k%28k%2B1%29%282k%2B1%29%29%2F6+%2B+%28k%2B1%29%5E2 becomes
(2k^3+9k^2+13k+6)/6

Now I am looking for one of the factors to be (k+1), so divide this into the numerator...it divides exactly, as I would expect, to leave 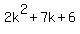2k%5E2%2B7k%2B6 which then factorises to give, fully,

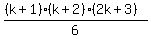
%28%28k%2B1%29%28k%2B2%29%282k%2B3%29%29%2F6

Right, nearly there.
The first term is fine.
The second term can be written as (k+1) + 1
the third term can be written as 2(k+1)+1... just make sure you are happy that this is equivalent to 2k+3.

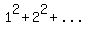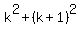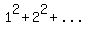so, we have proved that 1%5E2+%2B+2%5E2+%2B+... + k%5E2+%2B+%28k%2B1%29%5E2 gives a formula of the same form as that for 1%5E2+%2B+2%5E2+%2B+... + k%5E2 by adding on the next term, namely (k+1), therefore QED.

jon.