SOLUTION: Square or Cube? Find at least one positive integral solution to the equation: (integral means x and y must be integers) (-x)²y - y³ = 105. Please explain your response, becau

    (-x)²y - y³ = 105
       x²y - y³ = 105
     y(x² - y²) = 105
y(x - y)(x + y) = 105

So we have three factors y, x-y, and x+y having
product 105.

Since 105 = 1·3·5·7 either one of those factors is 1 
or none are.

If none of the three are 1 then

{y, x-y, x+y} = {3,5,7}.  

x+y must be the largest, 7 so

{y, x-y} = {3,5}.

The sum of the two elements of the left set must equal the 
sum of the two elements on the right set, so

y + x-y = 3+5
      x = 8

But that's impossible since the largest factor x+y is only 7 

So one of those factors must be 1.  Let's try y=1

y(x - y)(x + y) = 105
1(x - 1)(x + 1) = 105
         x² - 1 = 105
             x² = 106
              x = √106
which is not an integer.  So the first factor y cannot be 1.

The largest factor x+y cannot be 1, so the second factor x-y must be 1, 
x-y = 1, so we have y = x-1,

Substituting that:

      y(x - y)(x + y) = 105
  (x - 1)(1)(x + x-1) = 105
      (x - 1)(2x - 1) = 105
         2x² - 3x + 1 = 105
       2x² - 3x - 104 = 0
         (x-8)(2x+13) = 0

So x - 8 = 0,  2x + 13 = 0 
       x = 8        2x = -13
                     x = 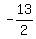 (discard)

So we have x = 8, and since y = x-1 = 8-1 = 7

So the only solution with positive integers is x = 8, y = 7.

Checking:

           (-x)²y - y³ = 105
           (-8)²7 - 7³ = 105
            64·7 - 343 = 105
             448 - 343 = 105
                   105 = 105

Edwin