SOLUTION: Dry sand is being poured into a conical pile at a rate of 10 cubic meters per minute; the diameter of the pile is equal to the height. At what rate is the height of the cone changi

Algebra ->  Rate-of-work-word-problems -> SOLUTION: Dry sand is being poured into a conical pile at a rate of 10 cubic meters per minute; the diameter of the pile is equal to the height. At what rate is the height of the cone changi      Log On


   

Question 745144: Dry sand is being poured into a conical pile at a rate of 10 cubic meters per minute; the diameter of the pile is equal to the height. At what rate is the height of the cone changing when there are 144π cubic meters of sand in the pile?
Answer by KMST(5328) About Me  (Show Source):
You can put this solution on YOUR website!
h= height of the cone = diameter of the base
The volume of a cone, V, is calculated as
V=%281%2F3%29%2AB%2Ah=%281%2F3%29%2Api%2Ar%5E2%2Ah based on the height and
B= area of the base, or r= radius of the base
In the case of the pile of sand, r=h%2F2, so

When V=144pi, %281%2F12%29%2Api%2Ah%5E3=144pi --> h%5E3=144%2A12=12%5E3 --> h=12

For all other times, solving for h we get
V=%281%2F12%29%2Api%2Ah%5E3 --> 12V%2Fpi=h%5E3 --> h=root%283%2C12V%2Fpi%29 or h=%2812V%2Fpi%29%5E%281%2F3%29
V is a linear function of time
If t time after V=144pi (with V in m%5E3 and t in minutes,
V=144pi%2B10t and
As h is not a linear function of time, the rate of change for h changes with time, and for an exact value we have to calculate it using calculus.
Without calculus, we can get approximate values.

WITH CALCULUS:
dh%2Fdt=%281%2F3%29%281728%2B120t%2Fpi%29%5E%28-2%2F3%29%2A%28120%2Fpi%29,
and at t=0,

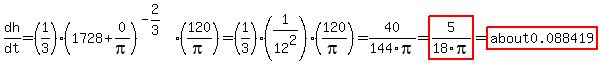
WITHOUT CALCULUS:
We can get estimates of the instantaneous rate of change in h when V=144pi by calculating the average rate of change over short periods of time, when V is about 144pi.
For example, between t=0 and t=0.1 minutes, V changes from
V%280%29=144pi to V%280.1%29=144pi%2B1 and h changes from
h%280%29=12 to h%280.1%29=%281728%2B12%2Fpi%29%5E%281%2F3%29=about12.00883543
The average rate of change is 0.00883543%2F0.1=0.0883543
If we use t=0 and t=0.01 with
h%280%29=12 and h%280.01%29=%281728%2B1.2%2Fpi%29%5E%281%2F3%29=about12.00088413,
we get an average rate of change of
0.00088413%2F0.01=0.88413
Either way, we see that highlight%280.884%29 meters per minute is a good estimate of the rate of increase for the height of the pile when V=144pi.

NOTE:
We did not really need to keep using V=%281%2F12%29%2Api%2Ah%5E3, or h=%2812V%2Fpi%29%5E%281%2F3%29, or h=%281728%2B120t%2Fpi%29%5E%281%2F3%29 to calculate an approximate rate of change without calculus. All we needed to know is that for V=144pi h=12.
We know that the ratio of volumes of similar solids is the cube of the ratio of lengths for any dimension measured, so
V%28t%29%2FV%280%29=%28h%28t%29%2Fh%280%29%29%5E3 <-->
That would let us calculate the height for any other volume
Since V%280.1%29=144pi%2B1, ,
V%280.1%29=V%280%29%2A0.000736286=12%2A0.000736286=12.00883543
and the average rate of change
%28h%280.1%29-h%280%29%29%2F%280.1-0%29=%2812.00883543-12%29%2F0.1=0.0883543