Question 744604: Which of the following relations is a function?
A.(2, 6), (3, 9), (4, 2), (3, 6)
B.(2, 8), (3, 6), (2, 4), (0, 2)
C.(3, -2), (4, 7), (-2, 5), (-4, 5)
D.(4, 7), (-2, 5), (1, 3), (-2, 1)
Found 2 solutions by lynnlo, MathLover1:
Answer by lynnlo(4176)   (Show Source): (Show Source):
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Relations and functions are very closely related. While all functions are relations, not all relations are functions. That's because functions are a special subset of relations.
For a relation to be a function, there must be 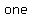 and and    value for value for   value. value.
If there are two pairs of numbers that have the 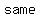  value but value but 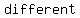  values, then the relation is values, then the relation is  a function. a function.
A.( , , ), ( ), ( , , ), ( ), ( , ,  ), ( ), ( , ,  ) )
since pairs ( , , ) and ( ) and ( , ,  ) have the ) have the 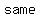  value but value but 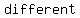  values, the relation is values, the relation is  a function a function
B.( , , ), ( ), ( , ,  ), ( ), ( , ,  ), ( ), ( , ,  ) )
( , , ), ( ), ( , , ), ( ), ( , ,  ), ( ), ( , ,  ) )
since pairs ( , , ) and ( ) and ( , , ) have the ) have the 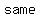  value but value but 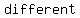  values, the relation is values, the relation is  a function a function
C.( , , ), ( ), ( , , ), ( ), ( , ,  ), ( ), ( , ,  ) )
since this relation has NO pairs that have the 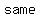  value but value but 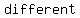  values, the relation values, the relation 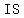 a function a function
D.( , ,  ), ( ), ( , ,  ), ( ), ( , ,  ), ( ), ( , ,  ) )
since pairs ( , , ) and ( ) and ( , ,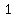 ) have the ) have the 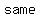  value but value but   values, the relation is values, the relation is  a function a function
so, your answer is : 
|
|
|