SOLUTION: Please help me determine two other angles that have the same trig ratio as sin 2.3. I dont know where to begin; can i switch the radian to a degree? Please help!!

Algebra ->  Trigonometry-basics -> SOLUTION: Please help me determine two other angles that have the same trig ratio as sin 2.3. I dont know where to begin; can i switch the radian to a degree? Please help!!      Log On


   

Question 744146: Please help me determine two other angles that have the same trig ratio as sin 2.3. I dont know where to begin; can i switch the radian to a degree? Please help!!
Found 2 solutions by lwsshak3, KMST:
Answer by lwsshak3(11628) About Me  (Show Source):
You can put this solution on YOUR website!
Please help me determine two other angles that have the same trig ratio as sin 2.3. I dont know where to begin; can i switch the radian to a degree?
***
using calculator set to radians:
sin(2.3)≈0.7457 (in quadrant II where sin>0)
sin(π-2.3)=sin(.8416)≈0.7457 (in quadrant I where sin>0)
sin (π+2.3)=sin(5.4416)≈-0.7457 (in quadrant III where sin<0)
sin(2π-2.3)=sin(3.9832)≈-0.7457 (in quadrant IV where sin<0)

Answer by KMST(5328) About Me  (Show Source):
You can put this solution on YOUR website!
You could switch radians to degrees, but that would not help if the answer is expected in radians.

MATCHING JUST SINE:
The sine of supplementary angles is the same. For example,
sin%2830%5Eo%29=sin%28180%5E0-30%5Eo%29=sin%28150%5E0%29=0.5
and all the angles differing by 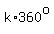k%2A360%5Eo from those have the same sine too.

2pi radians corresponds to 360%5Eo,
pi radians corresponds to 180%5Eo, and
pi%2F2 radians corresponds to 90%5Eo.
pi%2F2%3C2.3%3Cpi so an angle of 2.3 radians is in the second quadrant.
There is a supplementary first quadrant angle that has the same sine: pi-2.3.
All the angles that differ from those by a whole number of turns (clockwise or counterclockwise) have the same sine too, so adding or subtracting 2pi to the previous answers gives you more answers:
2pi%2B2.3, 2.3-2pi, 3pi-2.3, -2.3-pi
If you want to translate 2.3 radians to degrees, knowing that pi radians corresponds to 180%5Eo, you can calculate that 2.3 radians corresponds to
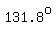2.3%2A180%5Eo%2Fpi= approximately 131.8%5Eo (rounding to the nearest 0.1%5Eo)

IF YOU HAVE TO MATCH ALL TRIG RATIOS:
The angles that have all the same trigonometric ratios are the co-terminal angles, those that differ by multiples of 360%5Eo or 2pi.
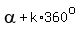So, for an angle alpha (in degrees), all angles measuring alpha%2Bk%2A360%5Eo for some positive or negative integer k have all the same trigonometric ratios.
Thinking in radians, for an angle theta (in radians), all angles measuring theta+%2Bk%2A2pi for some positive or negative integer k have all the same trigonometric ratios.