Question 74399This question is from textbook Prentice Hall Algebra 1 Practice Workbook
: 1. Twenty more than the square of a number is twelve times the number. find the numbers.
______________________________________________________________________________
2. The Product of three more than a number times two less than the number is fourteen. Find the numbers.
____________________________________________________________________________
3. The sum of the squares of two consecutive odd positive integers is 202. Find the numbers.
This question is from textbook Prentice Hall Algebra 1 Practice Workbook
Answer by bucky(2189)   (Show Source): (Show Source):
You can put this solution on YOUR website! Problem 1: Twenty more than the square of a number is twelve times the number. find the numbers.
.
Begin by calling the unknown number or numbers N. Squaring N gives you 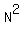 and and
20 more than that is 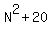 . The problem then tells you that this equals 12 times . The problem then tells you that this equals 12 times
the number which is written as 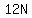 . So the equation becomes: . So the equation becomes:
.

.
Get this into the standard form of a quadratic equation by subtracting 12N from both sides.
The result is:
.

.
The left side of this equation can be factored into two terms as follows:
.

.
(You can check this by multiplying these two terms and seeing that they get you back to
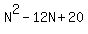 .) .)
.
Notice that the factored form of the equation will be true if either  or if or if
 because if either factor equals zero, the entire left side of the equation because if either factor equals zero, the entire left side of the equation
equals zero.
.
So, one at a time set the two factors equal to zero and solve for N. From the first factor
you will find that  and from the second factor you will find that and from the second factor you will find that  . .
So your problem has two answers that work ... N = 10 and N = 2. Check these two out by
returning to the problem and asking yourself, "Does 20 more than the square of 10 equal
12 times 10?" This simplifies to, "Does 20 more than 100 equal 120?" and, of course, it
does. Then you can do the same with 2. "Does 20 more than the square of 2 equal
12 times 2?" This simplifies to, "Does 20 more than 4 equal 24?" and, of course, it does also.
.
Problem 2: The Product of three more than a number times two less than the number is
fourteen. Find the numbers.
.
Again, let N represent the unknown number or numbers. Three more than that number is
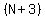 and two less than that number is and two less than that number is 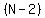 . The problem says that product of . The problem says that product of
these two quantities equals 14. In equation form this becomes:
.

.
Multiply out the left side and the equation becomes:
.

.
Put this into standard quadratic form by subtracting 14 from both sides to eliminate
the 14 on the right side of the equation. The result of this subtraction from both sides is:
.

.
The left side of this equation factors and the factored form is:
.

.
Just as we did in the first problem (and for the same reason) set each of the factors equal
to zero and you find that  and and  are the two solutions. are the two solutions.
.
Check by determining if (-5+3)*(-5-2) equals 14. (It does). And then determine if
(4+3)*(4-2) equals 14. (It does also).
.
Problem 3: The sum of the squares of two consecutive odd positive integers is 202. Find
the numbers.
.
Let N represent the odd positive integer. Then the next odd positive integer must be
N+2 because odd integers are always separated by an even integer in between. [Think that
two odd integers in a row are 3 and 5 or 7 and 9. They are always 2 apart.]
.
The squares of these two integers are 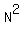 and and 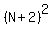 which is equal to which is equal to
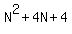 . When you add these two squares together you get: . When you add these two squares together you get:
.
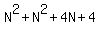 and by combining the squared terms this becomes: and by combining the squared terms this becomes:
.
 . Set this sum of the squares equal to 202 as required by the problem. . Set this sum of the squares equal to 202 as required by the problem.
.

.
Then get this into standard quadratic form by subtracting 202 from both sides to eliminate the
202 on the right side and the equation becomes:
.

.
Simplify the problem a little by dividing both sides (all terms) by 2 to eliminate the
multiplier of 2 on the 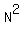 term and the equation reduces to: term and the equation reduces to:
.

.
This factors to:
.

.
Setting each factor equal to zero as was done in the other problems above results in
two answers:  and and  . The problem, however, requires the answer to . The problem, however, requires the answer to
be a positive odd number, so we ignore the negative answer for N and the answer to this
problem is that N = +9. The other positive odd integer is 2 plus the +9 or 11. In summary
the two odd positive integers you are looking for are 9 and 11.
.
Check by finding the sum of their squares. The squares are 81 and 121 and their sum is 202
as is required by the problem, so the answers we got check.
.
Hope that in these three problems you see how to work with setting up these quadratic
equations and you see how you can solve them by factoring, if they do factor. If they do not
factor you will have to use another method to solve them, and the most universal method is
the quadratic formula which is another lesson entirely.
|
|
|