12 boys and 8 men can finish a piece of work in 5 days.and 8 boys nd 6men can finish it in 7 days . find the time by 1 man alone and 1 boy alone to finish the work.
Suppose 1 boy alone can can do 1 job in b days.
Then 1 boy's work rate is 1 job per b days or 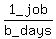 or
or 
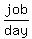 Then 12 boys' work rate is 12 times
Then 12 boys' work rate is 12 times 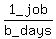 or
or 
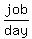 and 8 boys' work rate is 8 times
and 8 boys' work rate is 8 times 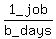 or
or 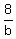
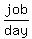 Suppose 1 man alone can can do 1 job in m days.
Then 1 man's work rate is 1 job per m days or
Suppose 1 man alone can can do 1 job in m days.
Then 1 man's work rate is 1 job per m days or 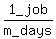 or
or 
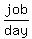 Then 8 men's work rate is 8 times
Then 8 men's work rate is 8 times 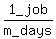 or
or 
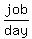 and 6 men's work rate is 6 times
and 6 men's work rate is 6 times 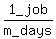 or
or 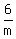
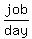
>>12 boys and 8 men can finish a piece of work in 5 days<<
So the combined work rate of 12 boys and 8 men is 1 job per 5 days or 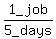 or
or 
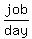 So we get one equation from
So we get one equation from










>>8 boys and 6 men can finish it in 7 days<<
So the combined work rate of 8 boys and 6 men is 1 job per 7 days or 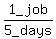 or
or 
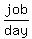
So we get the other equation from





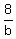

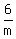


So we have the system of equations

IMPORTANT: DO NOT CLEAR OF FRACTIONS:
To eliminate the terms in m, multiply the first equation
through by 3, and multiply the second equation through
by -4:

Adding those equations term by term gives

NOW we can clear of fractions. Multiply both sides
by the LCD of 35b


So each boy will take 140 days.
Substitute 140 for b in



Multiply both sides by 10m


So each man will take 80 days.
Edwin