Question 743388: determine the smallest number which when divided by7,9and 11 leaves remainder 1,2and3 respectively with comlete process.
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website!  = the number we are looking for = the number we are looking for
 divided by 7 leaves a remainder of 1 can be written as divided by 7 leaves a remainder of 1 can be written as
 <--> <-->  for some integer for some integer 
In words, we would say 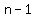 is a multiple of 7 (or is divisible by 7). is a multiple of 7 (or is divisible by 7).
If a larger number also leaves a remainder of 1 when divided by 7, then those numbers will differ by multiples of 7.
 divided by 9 leaves a remainder of 2, and divided by 9 leaves a remainder of 2, and
 divided by 11 leaves a remainder of 3 can be interpreted similarly divided by 11 leaves a remainder of 3 can be interpreted similarly
Since 7, 9, and 11 are relatively prime (no common factors), if a number is divisible by 7, 9, and 11, it must be divisible by  . .
We could say that  , , 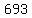 , ,  are exactly divisible by 7, 9, and 11. are exactly divisible by 7, 9, and 11.
If a number leaves remainders of 1,2, and 3 respectively when divided by 7, 9, and 11, adding (or subtracting) 693 to that number will produce another number that satisfies the same requirement.
The smallest such number must be between 0 and 693.
Let's consider numbers with a remainder of 3 when divided by 11.
We could say that the first number with a remainder of 3 when divided by 11 is 3, and adding 11 repeatedly we get others. The next is 14, then 25, and so on. It's an arithmetic sequence.
When divided by 7, and by 9, 3 leaves a remainder of 3.
In the sequence 3, 14,25, ..., the remainders from dividing by 9, and by 7 change in predictable ways.
The remainders from dividing by 9, increase by  each time to 5 and 7, and continue to increase in modulo 9 fashion to each time to 5 and 7, and continue to increase in modulo 9 fashion to  , ,  , ,  , ,  , ,  , ,  , and then , and then  starting the cycle again, after 9 additions of 11 for a total addition of starting the cycle again, after 9 additions of 11 for a total addition of  when divided by 9 is when divided by 9 is  . Every . Every 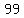 units we get another one. units we get another one.
The remainders from dividing by 7, increase by  each time in modulo 7 fashion going to each time in modulo 7 fashion going to  , ,  , ,  , ,  , ,  , ,  and then and then  , starting the cycle again, after 7 additions of 11 for a total addition of , starting the cycle again, after 7 additions of 11 for a total addition of  when divided by 7 is when divided by 7 is  . Every . Every  units we get another one. units we get another one.
We need a number that can be written as  and as and as 
 --> --> --> --> --> 11(2p+1)=77q-77p}}}--> --> 11(2p+1)=77q-77p}}}-->
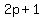 must be a multiple of 7, and the smallest one happens for must be a multiple of 7, and the smallest one happens for  --> -->

|
|
|