Question 742370: I measured the diameter of the central core of a roll of wrapping paper to be 3.8cm. I cut it along the spiral join and counted 8.5 spirals as i roll out the net. I measured the base angle to be 30 degrees.
I wondered how cardboard rolls were made. if i used a rectangular piece of cardboard to make one, i'd have some waste. What would be the smallest percentage of cardboard wasted if i made the core that i'd just cut up using a piece of rectangular cardboard?
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! NOTE: Since you are not specifying some overlap, I am assuming this is not a real life problem. In classroom problems, we assume that the edges can be somehow glued together without overlap. I will calculate that way.
I imagine the factory that makes those rolls cuts those strips of cardboard in large numbers, one next to the other, on a slant, from a long roll of cardboard.
If you tried to cut just one strip it the same way (on a slant) from a rectangle of cardboard, there would be a lot of waste:
  is the circumference of the roll, but it does not matter for the percentage waste. is the circumference of the roll, but it does not matter for the percentage waste. 
Your best bet for cutting just one strip would be to cut it along the length of a very long and thin cardboard rectangle, like this (drawing not to scale):
 L should have been much, much longer, but I chose to make it not to scale. L should have been much, much longer, but I chose to make it not to scale.
The waste in this case would be the two triangles at the ends.
Their total area is  . .
The area of the green cardboard rectangle used is 
The fraction wasted is 
and we can express all those lengths (L, x, c, and h) as a function of c.
We knew that  . .
We know that  , but I do not want to mess with that square root unless I have to. , but I do not want to mess with that square root unless I have to.
 and and  are the legs of those right triangles with hypotenuse c. are the legs of those right triangles with hypotenuse c.
 = = = =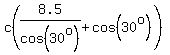 = =
Since  , ,
 = =
The wasted fraction is
 = = = = = = = =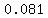 (rounded) (rounded)
That means that 8.1% of the long and thin cardboard rectangle would be wasted.
I don't think we can reduce the waste any further, but you would need a cardboard rectangle measuring  by by  . .
With  (rounded), that would be a strip 6cm wide by 127.5cm long. (rounded), that would be a strip 6cm wide by 127.5cm long.
|
|
|