Question 742270: please help me simplify these logarithms, I use  for logarithmic form , for logarithmic form ,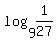 , , 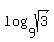 , , 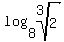 , and , and 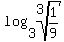
Found 2 solutions by stanbon, lwsshak3:
Answer by stanbon(75887)   (Show Source): (Show Source):
You can put this solution on YOUR website! log( 9, 1/27 ) = log(1/27)/log(9) = -3/2
-----------------------------------------------
log ( 9, sqrt( 3 ) ) = log(sqrt(3))/log(9) = (1/2)/2 = 1/4
-------------------------------------------------
log ( 8, root( 3, 2 )) =
log8(2^(1/3)) = log(2^(1/3))/log(2^3) = (1/3)/3 = 1/9
---------------------------------
log ( 3, root( 3, 1/9 ))}}}
log3[(1/9)^(1/3)] = log(1/9)^(1/3)/log(3) = (1/3)log(1/9)/log(3)
----
= (1/3)*(-2)/1 = -1/6
=============================
Cheers,
Stan H.
================
Answer by lwsshak3(11628)   (Show Source): (Show Source):
|
|
|