Question 742102: Respected Sir,
Please help me to solve:
If P(2n-1,n):P(2n+1,n-1) = 22:7 ,find n
Thank you in aniticipation
Answer by Edwin McCravy(20064)   (Show Source): (Show Source):
You can put this solution on YOUR website!
P(2n-1,n):P(2n+1,n-1) = 22:7
We can replace the colons by division symbols ÷
P(2n-1,n)÷P(2n+1,n-1) = 22÷7
P(2n-1,n)÷P(2n+1,n-1) =  Use the formula
P(a,b) =
Use the formula
P(a,b) =  P(2n-1,n)÷P(2n+1,n-1) =
P(2n-1,n)÷P(2n+1,n-1) = 
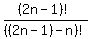 ÷ ÷ = =  Remove the inner parentheses in the denominators
Remove the inner parentheses in the denominators
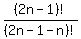 ÷ ÷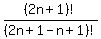 = =  Simplify by combining like terms:
Simplify by combining like terms:
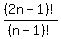 ÷ ÷ = =  On the left side, invert the second fraction and change
division to multiplication:
On the left side, invert the second fraction and change
division to multiplication:
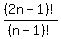 × × = =  Write (n+2)! as (n+2)(n+1)n(n-1)!
Write (2n+1)! as (2n+1)(2n)(2n-1)!
Write (n+2)! as (n+2)(n+1)n(n-1)!
Write (2n+1)! as (2n+1)(2n)(2n-1)!
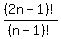 × ×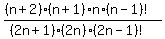 = =  Cancel the (2n-1)!'s
Cancel the (2n-1)!'s
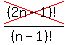 × ×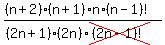 = =  Cancel the (n-1)!'s
Cancel the (n-1)!'s
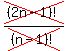 × ×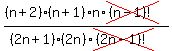 = =  Cancel the n's
Cancel the n's
 × ×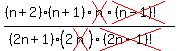 = =  All that's left is
All that's left is
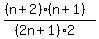 = =  Cross-multiply:
7(n+2)(n+1) = 22(2n+1)2
7(n²+3n+2) = 44(2n+1)
7n²+21n+14 = 88n+44
Get 0 on the right side:
7n²-67n-30 = 0
Factor the left side as
(n-10)(7n+3) = 0
Use the zero factor property:
n-10 = 0; 7n+3 = 0
n = 10; 7n = -3
n =
Cross-multiply:
7(n+2)(n+1) = 22(2n+1)2
7(n²+3n+2) = 44(2n+1)
7n²+21n+14 = 88n+44
Get 0 on the right side:
7n²-67n-30 = 0
Factor the left side as
(n-10)(7n+3) = 0
Use the zero factor property:
n-10 = 0; 7n+3 = 0
n = 10; 7n = -3
n = 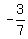 The original problem contained permutations,
which involves factorials. Only permutations
and factorials involving whole numbers are
defined, so we can discard the
The original problem contained permutations,
which involves factorials. Only permutations
and factorials involving whole numbers are
defined, so we can discard the 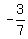 Solution: n = 10
Edwin
Solution: n = 10
Edwin
|
|
|