SOLUTION: I have a test tomorrow and my teacher has not explained trig functions well enough for me (or anyone else) to understand. We have been working on equations that involve sinx= 1/c

Algebra ->  Trigonometry-basics -> SOLUTION: I have a test tomorrow and my teacher has not explained trig functions well enough for me (or anyone else) to understand. We have been working on equations that involve sinx= 1/c      Log On


   

Question 741088: I have a test tomorrow and my teacher has not explained trig functions well enough for me (or anyone else) to understand. We have been working on equations that involve
sinx= 1/cscx cscx= 1/sinx cos2x+sin2x=1
tanx= 1/cotx cotx= 1/tanx etc.,
cosx= 1/secx secx= 1/cosx
I am wondering how to solve any equation, but I will provide a couple.
1)csc3x-csc2x-cscx+1
2)sin2x(-1+cos2x)
3)secx-sinxtanx
Thank you!
Answer by KMST(5328) About Me  (Show Source):
You can put this solution on YOUR website!
All the trigonometric functions can be expressed in terms of sin%28x%29 or cos%28x%29.
Sine and cosine are the lengths of the legs of a right triangle with hypotenuse measure 1, so the sum of their squares is 1.
That is usually written as:
sin%5E2%28x%29%2Bcos%5E2%28x%29=1 meaning %28sin%28x%29%29%5E2%2B%28cos%28x%29%29%5E2=1
The other trigonometric functions are very easily defined based on sine and cosine.
All you need to know is:
the relation of sine and cosine (see above),
the definition of tangent, cotangent, secant and cosecant based on sine and cosine,
and enough basic algebra.

IN GENERAL:
I would suggest expressing everything in terms of sin%28x%29 and cos%28x%29 and keeping your eyes open,
looking for expressions that can be simplified by using either the definition of one of the other functions,
or the relation of sine and cosine.
Keep your eyes open, because the relation of sine and cosine could be disguised by basic algebra manipulations:
sin%5E2%28x%29%2Bcos%5E2%28x%29=1<-->1-sin%5E2%28x%29=cos%5E2%28x%29<-->-1%2Bsin%5E2%28x%29=-cos%5E2%28x%29
sin%5E2%28x%29%2Bcos%5E2%28x%29=1<-->1-cos%5E2%28x%29=sin%5E2%28x%29<-->-1%2Bcos%5E2%28x%29=-sin%5E2%28x%29

2) sin%5E2%28x%29%28-1%2Bcos%5E2%28x%29%29
That expression in parenthesis with a squared cosine is asking you to use the relation between sine and cosine.
-1%2Bcos%5E2%28x%29=-sin%5E2%28x%29 so


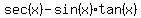
3) sec%28x%29-sin%28x%29%2Atan%28x%29
Expressing everything based on sine and cosine, we get
sec%28x%29-sin%28x%29%2Atan%28x%29=1%2Fcos%28x%29-sin%28x%29%2A%28sin%28x%29%2Fcos%28x%29%29
Now a little basic algebra:

Next, you have to recognize the numerator as 1-sin%5E2%28x%29=cos%5E2%28x%29, and simplify a little further:


1) csc%5E3%28x%29-csc%5E2%28x%29-csc%28x%29%2B1
The best I can do with that is

Factoring the polynomial first saved time.
It is the same as factoring y%5E3-y%5E2-y%2B1=%28y%5E2-1%29%28y-1%29.