Question 74086: Hi, could you help me with this problem please?
Find the geometric mean between 2sqrt2 and 6sqrt6.
I don't know how to solve this problem.
Thank you!
Found 2 solutions by stanbon, bucky:
Answer by stanbon(75887)   (Show Source): (Show Source):
You can put this solution on YOUR website! Find the geometric mean between 2sqrt2 and 6sqrt6.
I don't know how to solve this problem.
----------
If a and b are numbers then x is the geometric mean
if a/x = x/b or x=sqrt(ab)
---------------
So, geo mean = sqrt(2sqrt2*6sqrt6)=sqrt(12sqrt12)
=sqrt(24sqrt3)
=sqrt24)(3^1/4)
= 2(sqrt6)(3^1/4)
= 2*(3^(1/4)(sqrt6)
=========
Cheers,
Stan H.
Answer by bucky(2189)   (Show Source): (Show Source):
You can put this solution on YOUR website! If you are given two numbers x and y, the geometric mean between those two numbers is defined
as  and and 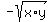 . .
.
This means that you just multiply the two given numbers together, take the square root of
the product, simplify the answer, and precede it by a plus-minus sign or write it as
2 identical answers except that one has a plus sign and the other has a minus sign.
.
In this problem you are given the two numbers  and and  . .
If you
multiply these two together you get:
.
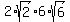
.
The 2 and the 6 multiply to give 12 and the multiplication 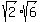 equals equals 
.
At this stage the answer is 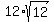 . But the radical term can be simplified as . But the radical term can be simplified as
follows:
.
 . Substituting this for . Substituting this for  leads leads
to the product being:
.
 which further simplifies to which further simplifies to 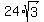
.
This is now the product that you take the square root of. So you now need to find:
.

.
This can be split into
.
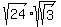
.
One factor at a time. First 
.

.
Now for the second term 
.
Note that taking the square root of the square root of three is the same as:
 which becomes which becomes 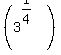 . .
.
So now our geometric mean (both factors together) has become:
.
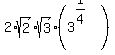
.
Change the  to exponential form: to exponential form:  . Multiply this by the . Multiply this by the
other exponential form of 3 (remember multiplying means adding exponents) to get:
.

.
Finally, 
.
Substitute this and the geometric mean becomes:
.
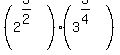 <--- if the numerators in the exponents are cut off by the print generator, <--- if the numerators in the exponents are cut off by the print generator,
be aware that the exponents are (3/2) and (3/4).
.
and don't forget to add the plus-minus sign in front or to make a pair of answers, one
with a plus sign and the same answer with a minus sign.
.
A math nightmare! I hope you could follow the twists and turns of the simplification
process. The most important thing to understand from this problem is the definition
of geometric mean for two terms and how you apply four steps ... multiply, take the square root of
the product, simplify the result, and add the plus-minus sign. The rest is all algebraic manipulation.
|
|
|