SOLUTION: For each rational function, identify any holes or horizontal or vertical asymptotes of its graph. 1) y= (x+3)/(x+2)(x+3) 2) y= x+5/(x-2)(x-3)

Algebra ->  Trigonometry-basics -> SOLUTION: For each rational function, identify any holes or horizontal or vertical asymptotes of its graph. 1) y= (x+3)/(x+2)(x+3) 2) y= x+5/(x-2)(x-3)      Log On


   

Question 740836: For each rational function, identify any holes or horizontal or vertical asymptotes of its graph.
1) y= (x+3)/(x+2)(x+3)
2) y= x+5/(x-2)(x-3)
Answer by MathLover1(20850) About Me  (Show Source):
You can put this solution on YOUR website!
1) y=+%28x%2B3%29%2F%28%28x%2B2%29%28x%2B3%29%29
y=+cross%28%28x%2B3%29%291%2F%28%28x%2B2%29cross%28%28x%2B3%29%29%29
y=+1%2F%28x%2B2%29


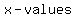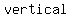Vertical asymptotes will occur for x-values which make the denominator zero. For this equation the denominator will be zero if x+=+-2 . So the vertical lines, x+=-+2 will be vertical+asymptote for this equation.
For this equation, when 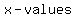x-values become very large, the fraction approaches zero in value.
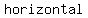so, y=0 is horizontal asymptote




2.
y=+%28x%2B5%29%2F%28%28x-2%29%28x-3%29%29 or
y=%28x%2B5%29%2F%28x%5E2-5x%2B6%29

"Holes" would occur when the numerator and denominator have a common factor which is an expression which could be zero.
Since this fraction has no such common+factors, there will be no "holes".
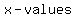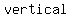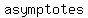Vertical asymptotes will occur for x-values which make the denominator zero. For this equation the denominator will be zero if x+=+2 or x+=+3. So the vertical lines, x+=+2 and x+=+3 will be vertical+asymptotes for this equation.
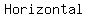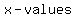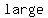Horizontal asymptotes will occur if y approaches some constant value when x-values become very+large (positive or negative).
For this equation, when 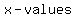x-values become very large, the denominator of the fraction becomes very large.
This makes the fraction very, very 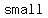small. In fact the fraction approaches zero in value.
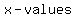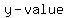So as x-values become very large, the fraction becomes negligible and the y-value approaches x=0.