Question 739216: ankita travel 14 km to home partially by rickshaw AND BY BUS SHE TAKES 1 2 HR IF SHE TRAVELS BY RICKSHAW AND THE REMAING DISTANCE BY BUS ON OTHER HAND IF SHE TRAVELS 4 KM BY RICKSHAW AND REMAING DISTANCE BY BUS SHE TAKES 9 MINUTES LONGER
Answer by ankor@dixie-net.com(22740)   (Show Source): (Show Source):
You can put this solution on YOUR website! Will try to make sense of this.
:
Ankita travel 14 km home, partially by rickshaw and by bus.
:
She takes  hr if is she travels 4 km by Rickshaw and takes the remaining distance by by bus. hr if is she travels 4 km by Rickshaw and takes the remaining distance by by bus.
:
On the other hand, if she travels 10 km by rickshaw, and the remaining distance by bus, she takes 9 min longer.
:
Assume you want to find the speed of the rickshaw and speed of the bus.
:
let r = speed of the rickshaw
let b = speed of the bus
:
Write an time equation for the 1st statement (time = dist/speed):
"She takes  hr if is she travels 4 km by Rickshaw and takes the remaining distance by by bus." hr if is she travels 4 km by Rickshaw and takes the remaining distance by by bus."
 + + 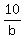 = = 
multiply equation by 2rb, to get rid of the denominators
2rb* + 2rb* + 2rb*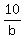 = 2rb* = 2rb*
cancel the denominators
8b + 20r = rb
:
Write a time equation for the 2nd statement (time = dist/speed):
"if she travels 10 km by rickshaw, and the remaining distance by bus, she takes 9 min longer."
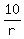 + +  = 30 + 9 = 30 + 9
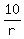 + +  = 39 = 39
change 39 min to hr (we're finding the speed in km/hr
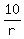 + +  = = 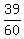
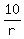 + +  = = 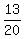
multiply equation by 20rb, to get rid of the denominators
20rb*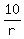 + 20rb* + 20rb* = 20rb* = 20rb*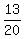
cancel the denominators
200b + 80r = 13rb
:
multiply the first equation by 4, subtract from the above equation
200b + 80r = 13rb
32b + 80r = 4rb
-----------------
168b = 9rb
divide both sides by by b
168 = 9r
r = 168/9
r = 18.67 km/hr is the speed of the rickshaw (Is that possible?)
:
Find the speed of the bus
8b + 20r = rb
8b + 20(18.67) = 18.67b
373.3 = 18.67b - 8b
373.3 = 10.67b
b = 373.3/10.67
b ~ 35 km/hr is the speed of the bus
:
:
See if that checks out in the first statement, find the travel time of each
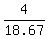 + + 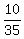 = =
.214 + .286 = .5 hrs
|
|
|