Question 73908This question is from textbook
: Find all solutions to the equation sin x = 0.
a. x = 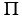 n n
b. x = 2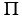 n n
c. x = 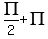 n n
d. x = 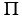 + 2 + 2 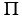 n
This question is from textbook n
This question is from textbook
Answer by bucky(2189)   (Show Source): (Show Source):
You can put this solution on YOUR website! Find all solutions to sin x = 0
.
Answer "a" is the correct selection for this problem.
.
Probably the best way to work this problem is to look at the answers and evaluate them one at
a time to see if the sine they produce actually does equal zero.
.
Another thing that might help you is to recognize that  is equivalent to 180 degrees. is equivalent to 180 degrees.
.
It always helped me to use the definitions of trig functions to evaluate the values of
those functions. For example, in this problem you are interested in the sine function
and it is defined as the ratio of the side opposite divided by the hypotenuse. So when will
the sine be equal to zero? That will occur when the side opposite disappears and thinking
of the angle being in standard position in the first quadrant, the side opposite gets smaller
and smaller as the angle goes towards 0 degrees (or 0 radians). The sine finally reaches
0 at 0 degrees or zero radians. The same thing happens as the angle approaches pi radians
or 180 degrees. The side opposite approaches 0 until at pi radians or 180 degrees it
actually is 0 and therefore the  . .
.
Another way you can view this is to think of the sine wave plot. It starts at 0, rises to
a peak at  or 90 degrees, then falls back to zero at or 90 degrees, then falls back to zero at  or 180 degrees, or 180 degrees,
then falls further to a minimum at  or 270 degrees and then rises to again be zero or 270 degrees and then rises to again be zero
at  or 360 degrees. or 360 degrees.
.
So we have sin(x) equal to zero at 0 and  or 180 degrees and or 180 degrees and  or 360 degrees or 360 degrees
and every additional  or 180 degrees thereafter. or 180 degrees thereafter.
.
Note that answer "a" meets that requirement as long as n = 0,1,2,3,4,5,...
.
Answer b will not work because it is multiples of  . When n = 0 it works, but . When n = 0 it works, but
when n = 1 it is at  or 360 degrees. It completely skipped over the fact that or 360 degrees. It completely skipped over the fact that
 . .
.
Answer c will not work. When n = 0 the angle is  or 90 degrees. The value of or 90 degrees. The value of
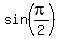 or its equivalent or its equivalent 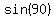 is 1, not zero. is 1, not zero.
.
Answer d will not work. When n = 0 the angle becomes  (or 180 degrees) and for each (or 180 degrees) and for each
increase in n you add  or 360 degrees. So the angles it generates are or 360 degrees. So the angles it generates are  (180 degrees), (180 degrees),
 (540), (540), 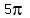 (900) ... It completely misses the angles 0, (900) ... It completely misses the angles 0,  (360 degrees), (360 degrees),
 (720), (720),  (1080) ... (1080) ...
.
Hope this discussion helps you to become more familiar with trig functions and angles.
|
|
|