SOLUTION: I need help finding a) vertex b) vertices c) foci d) major axis and e) minor axis of the ellipse: 9x^2-18x+4y^2-27=0

Algebra ->  Quadratic-relations-and-conic-sections -> SOLUTION: I need help finding a) vertex b) vertices c) foci d) major axis and e) minor axis of the ellipse: 9x^2-18x+4y^2-27=0       Log On


   

Question 738632: I need help finding a) vertex b) vertices c) foci d) major axis and e) minor axis of the ellipse: 9x^2-18x+4y^2-27=0
Answer by Ed Parker(21) About Me  (Show Source):
You can put this solution on YOUR website!

The idea is to get the equation like one of these

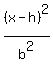
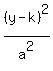
%28x-h%29%5E2%2Fa%5E2%22%22%2B%22%22%28y-k%29%5E2%2Fb%5E2%22%22=%22%221 or %28x-h%29%5E2%2Fb%5E2%22%22%2B%22%22%28y-k%29%5E2%2Fa%5E2%22%22=%22%221

a is one-half the major axis and b is one-half the minor axis.
So a² is always larger than b².  If a² is under the term in x,
the ellipse is like this: drawing%2820%2C10%2C-2%2C2%2C-1%2C1%2Carc%280%2C0%2C-3.9%2C1.9%29+%29 and if b² is under the term in x, 
the ellipse looks like this drawing%2810%2C20%2C-1%2C1%2C-2%2C2%2Carc%280%2C0%2C1.9%2C-3.9%29+%29.
 
 9x² - 18x + 4y² - 27 = 0
 
Add 28 to both sides to get the constant 
term off the left side:

      9x² - 18x + 4y² = 27

Factor 9 out of of the first two terms:

     9(x² - 2x) + 4y² = 27

Complete the square in the parentheses:
1. Multiply the coefficient of x, which is -2 
   by 1%2F2, getting -1
2. Square -1, getting (-1)² or +1
3. Add +1 to the expression in the parentheses.
4. Since the parentheses is multiplied by 9,
   this amouts to adding 9 to the left side,
   so we must add 9·1 or 9 to the right side.

 9(x² - 2x + 1) + 4y² = 27 + 9

We factor x² - 2x + 1 as (x - 1)(x - 1) and as (x - 1)²

      9(x - 1)² + 4y² = 36

There is no y term so we do not need to complete
the square.  We just write y as (y - 0)

9(x - 1)² + 4(y - 0)² = 36  

Next we get 1 on the right side by dividing every 
term by 36

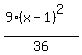
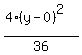
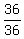     %289%28x-1%29%5E2%29%2F36%22%22%2B%22%22%284%28y-0%29%5E2%29%2F36%22%22=%22%2236%2F36

Simplify:

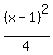
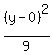
     %28x-1%29%5E2%2F4%22%22%2B%22%22%28y-0%29%5E2%2F9%22%22=%22%221

Since 4 is less than 9 we know that b²=4 is under the 
term in x, so the ellipse looks like this drawing%2810%2C20%2C-1%2C1%2C-2%2C2%2Carc%280%2C0%2C1.9%2C-3.9%29+%29.  We compare that to

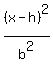
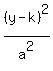
     %28x-h%29%5E2%2Fb%5E2%22%22%2B%22%22%28y-k%29%5E2%2Fa%5E2%22%22=%22%221

and get h=1, b²=4, k=0, a²=9, and of course b=2 and a=3

So the center = (h,k) = (1,0), the major axis is vertical, a=3 units
above the center and a=3 units below the center, like this green line,
which is the whole major axis:



The minor axis is horizontal, b=2 units left of the center and b=2
units right of the center, like this green line, which is the whole
minor axis:



So we can sketch in the ellipse:



 To calculate the foci, we need the quantity c, the distance
from the center to the foci, given by the equation:

c² = a² - b²
c² = 9 - 4
c² = 5
 c = √5

So the foci are the points (1,±√5)

The foci are plotted below:



The center is (1,0). The vertices are (1,±3).
the covertices are (-1,0) and (3,0),
the major axis is 6, the minor axis is 4.

Edwin